Archivo:Cuboedro Triangular.gif
No se dispone de una resolución más alta.
Cuboedro_Triangular.gif (492 × 480 píxeles; tamaño de archivo: 2,74 MB; tipo MIME: image/gif, bucleado, 110 frames, 8,9s)
Resumen
| Descripción |
Español: El cuboedro triangular: es un politopo tridimensional convexo, que posee 12 aristas intermedias primarias, 24 aristas intermedias segundarias y 72 aristas intermedias terciarias, para una suma total de 108 aristas intermedias. Además tiene ochos vértices intermedios primarios, seis vértices intermedios segundarios y vente y cuatros vértices intermedios terciarios, para la suma total de treinta y ochos vértices intermedios. Este poliedro posee 48 caras triangulares que son triángulos escalenos y 24 caras son triángulos isósceles de Jose. Esto son los treinta y ocho vértices del cuboedro triangular: V1 (-2.5, 2.5, 2.5), V2 (2.5, 2.5, 2.5), V3 (2.5, -2.5, 2.5), V4 (-2.5,- 2.5, 2.5), V5 (-2.5, 2.5, -2.5), V6 (-2.5, -2.5, -2.5), V7 (2.5, -2.5, -2.5), V8 (2.5, 2.5, -2.5), V9 (0, 0, 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0,0), V14 (0, 0, -4), V15 (0, 1.74, 3.12), V16 (-1.74, 0, 3.12), V17 (0, -1.74, 3.12), V18 (1.74, 0, 3.12), V19 (0, 1.74, -3.12), V20 (0, -1.74, -3.12), V21 (1.74, 0, -3.12), V22 (-1.74, 0, -3.12), V23 (-1.74, -3.12, 0), V24 (1.74, -3.12, 0), V25 (0, -3.12, -1.74), V26 (0, -3.12, 1.74), V27 (0, 3.12, 1.74), V28 (0, 3.12, -1.74), V29 (-1.74, 3.12, 0), V30 (1.74, 3.12, 0), V31 (3.12, -1.74, 0), V32 (3.12, 1.74, 0), V33 (3.12, 0, 1.74), V34 (3.12, 0, -1.74), V35 (-3.12, 1.74, 0), V36 (-3.12, -1.74, 0), V37 (-3.12, 0, -1.74), V38 (-3.12, 0, 1.74). Las aristas intermedias se clasifican en: 1) Aristas intermedias Primarias: son un conjunto de aristas que están visible en el poliedro seleccionado, con las cuales podemos formar un poliedro regular convexo. A1= conjunto de aristas primarias, G = cantidad de aristas primarias, A1= G. 2) Aristas intermedias secundarias: son un conjunto de aristas que están definida desde un vértice intermedio primario, hasta un vértice intermedio segundario. A2= conjunto de aristas secundaria, G = cantidad de aristas primarias, A2= 2G. 3) Arista intermedias terciarias: son un conjunto de aristas que están colocadas entre dos aristas intermedias secundarias, o entre una arista intermedia primaria y una arista intermedia secundaria. A3= conjunto de aristas terciarias, G = cantidad de aristas primarias, A3= 6G).
Además posee tres tipos de vértices intermedios: a) Vértices intermedio primario: son el conjunto de vértices intermedios que están definidos por un conjuntos de aristas intermedias primarias, las cuales definen un poliedro regular convexo. El cuboedro triangular posee (8) ochos vértices intermedios primarios, que en este caso están definidos por ochos tríos cartesianos. Ejemplo: V1 (-2.5, 2.5, 2.5), V2 (2.5, 2.5, 2.5), V3 (2.5, -2.5, 2.5), V4 (-2.5,- 2.5, 2.5), V5 (-2.5, 2.5, -2.5), V6 (-2.5, -2.5, -2.5), V7 (2.5, -2.5, -2.5), V8 (2.5, 2.5, -2.5). Estos ochos vértices intermedios primarios definen perfectamente un hexaedro regular convexo. b) Vértices intermedio secundario: son el conjunto de vértices intermedios que están definidos por un conjunto de aristas intermedias secundarias y en algunos casos están definidos por un conjunto de aristas misceláneas, de las cuales las aristas intermedias secundarias son parte fundamentales de este conjunto de aristas misceláneas. Con el conjunto de vértices intermedios segundario siempre se puede formar un poliedro regular convexo. Estos seis tríos cartesiano definen perfectamente un octaedro regular convexo, ejemplo: V9 (0, 0, 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0,0), V14 (0, 0, -4). c) Vértices intermedio terciarios: son el conjunto de vértices intermedios que están definidos por tres o más aristas terciarias, los cuales posen la cualidad de no definir un poliedro regular convexo. Con el conjunto de vértices intermedios terciarios en algunos casos podemos definir perfectamente unos de los poliedros de Arquímedes. Ejemplo: V15 (0, 1.74, 3.12), V16 (-1.74, 0, 3.12), V17 (0, -1.74, 3.12), V18 (1.74, 0, 3.12), V19 (0, 1.74, -3.12), V20 (0, -1.74, -3.12), V21 (1.74, 0, -3.12), V22 (-1.74, 0, -3.12), V23 (-1.74, -3.12, 0), V24 (1.74, -3.12, 0), V25 (0, -3.12, -1.74), V26 (0, -3.12, 1.74), V27 (0, 3.12, 1.74), V28 (0, 3.12, -1.74), V29 (-1.74, 3.12, 0), V30 (1.74, 3.12, 0), V31 (3.12, -1.74, 0), V32 (3.12, 1.74, 0), V33 (3.12, 0, 1.74), V34 (3.12, 0, -1.74), V35 (-3.12, 1.74, 0), V36 (-3.12, -1.74, 0), V37 (-3.12, 0, -1.74), V38 (-3.12, 0, 1.74). Estos 24 vértices intermedios forman perfectamente el poliedro de Arquímedes llamado Octaedro truncado.
English: he triangular cubohedron: it is a three-dimensional convex polytope, which has 12 primary intermediate edges, 24 secondary secondary edges and 72 tertiary intermediate edges, for a total sum of 108 intermediate edges. It also has eight primary intermediate vertices, six secondary and vertex intermediate vertices and four tertiary intermediate vertices, for the total sum of thirty-eight intermediate vertices. This polyhedron has 48 triangular faces that are scalene triangles and 24 faces are Jose's isosceles triangles. This is the thirty-eight vertices of the triangular cubohedron: V1 (-2.5, 2.5, 2.5), V2 (2.5, 2.5, 2.5), V3 (2.5, -2.5, 2.5), V4 (-2.5, - 2.5, 2.5) , V5 (-2.5, 2.5, -2.5), V6 (-2.5, -2.5, -2.5), V7 (2.5, -2.5, -2.5), V8 (2.5, 2.5, -2.5), V9 (0, 0 , 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0,0), V14 (0, 0, -4 ), V15 (0, 1.74, 3.12), V16 (-1.74, 0, 3.12), V17 (0, -1.74, 3.12), V18 (1.74, 0, 3.12), V19 (0, 1.74, -3.12), V20 (0, -1.74, -3.12), V21 (1.74, 0, -3.12), V22 (-1.74, 0, -3.12), V23 (-1.74, -3.12, 0), V24 (1.74, -3.12, 0), V25 (0, -3.12, -1.74), V26 (0, -3.12, 1.74), V27 (0, 3.12, 1.74), V28 (0, 3.12, -1.74), V29 (-1.74, 3.12, 0), V30 (1.74, 3.12, 0), V31 (3.12, -1.74, 0), V32 (3.12, 1.74, 0), V33 (3.12, 0, 1.74), V34 (3.12, 0, -1.74), V35 (-3.12, 1.74, 0), V36 (-3.12, -1.74, 0), V37 (-3.12, 0, -1.74), V38 (-3.12, 0, 1.74). The intermediate edges are classified into: 1) Primary intermediate edges: they are a set of edges that are visible in the selected polyhedron, with which we can form a regular convex polyhedron. A1 = set of primary edges, G = number of primary edges, A1 = G. 2) Secondary intermediate edges: a set of edges that are defined from a primary intermediate vertex, to a secondary intermediate vertex. A2 = set of secondary edges, G = number of primary edges, A2 = 2G. 3) Tertiary intermediate edges: they are a set of edges that are placed between two secondary intermediate edges, or between a primary intermediate edge and a secondary intermediate edge. A3 = set of tertiary edges, G = number of primary edges, A3 = 6G).
It also has three types of intermediate vertices: a) Primary intermediate vertices: they are the set of intermediate vertices that are defined by a set of primary intermediate edges, which define a regular convex polyhedron. The triangular cubohedron has (8) eight primary intermediate vertices, which in this case are defined by eight Cartesian triplets. Example: V1 (-2.5, 2.5, 2.5), V2 (2.5, 2.5, 2.5), V3 (2.5, -2.5, 2.5), V4 (-2.5, - 2.5, 2.5), V5 (-2.5, 2.5, - 2.5), V6 (-2.5, -2.5, -2.5), V7 (2.5, -2.5, -2.5), V8 (2.5, 2.5, -2.5). These eight primary intermediate vertices perfectly define a regular convex hexahedron. b) Secondary intermediate vertices: they are the set of intermediate vertices that are defined by a set of secondary intermediate edges and in some cases are defined by a set of miscellaneous edges, of which the secondary intermediate edges are a fundamental part of this set of edges miscellaneous. With the set of intermediate intermediate vertices a regular convex polyhedron can always be formed. These six cartesian trios perfectly define a regular convex octahedron, example: V9 (0, 0, 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0,0), V14 (0, 0, -4). c) Tertiary intermediate vertices: they are the set of intermediate vertices that are defined by three or more tertiary edges, which have the quality of not defining a regular convex polyhedron. With the set of tertiary intermediate vertices in some cases we can perfectly define some of the Archimedes polyhedra. Example: V15 (0, 1.74, 3.12), V16 (-1.74, 0, 3.12), V17 (0, -1.74, 3.12), V18 (1.74, 0, 3.12), V19 (0, 1.74, -3.12), V20 (0, -1.74, -3.12), V21 (1.74, 0, -3.12), V22 (-1.74, 0, -3.12), V23 (-1.74, -3.12, 0), V24 (1.74, -3.12, 0), V25 (0, -3.12, -1.74), V26 (0, -3.12, 1.74), V27 (0, 3.12, 1.74), V28 (0, 3.12, -1.74), V29 (-1.74, 3.12, 0), V30 (1.74, 3.12, 0), V31 (3.12, -1.74, 0), V32 (3.12, 1.74, 0), V33 (3.12, 0, 1.74), V34 (3.12, 0, -1.74), V35 (-3.12, 1.74, 0), V36 (-3.12, -1.74, 0), V37 (-3.12, 0, -1.74), V38 (-3.12, 0, 1.74). These 24 intermediate vertices perfectly form the Archimedes polyhedron called Truncated Octahedron.
Français : Le cuboedro triangulaire: un trois bords convexes de polytope dimensions 12 arêtes primaires intermédiaires possédant, intermédiaires 24 et 72 tertiaire segundarias bords intermédiaires, pour un total de 108 arêtes intermédiaires. Il a également huit sommets primaires intermédiaires, six sommets intermédiaires et quatre secondaires et tertiaires viennent sommets intermédiaires, à la somme totale de trente-huit sommets intermédiaires. Ce polyèdre a 48 faces triangulaires sont des triangles scalènes et 24 faces triangles isocèles sont Jose. Ce sont les trente-huit sommets du triangle cuboedro: V1 (-2,5, 2,5, 2,5), V2 (2,5, 2,5, 2,5), V3 (2,5, -2,5, 2,5), V4 (-2,5, - 2,5, 2,5) , V5 (-2,5, 2,5, -2,5), V6 (-2,5, -2,5, -2,5), V7 (2,5, -2,5, -2,5), V8 (2,5, 2,5, -2,5), V9 (0, 0 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0.0), V14 (0, 0, -4 ), V15 (0, 1,74, 3,12), V16 (-1,74, 0, 3.12), V17 (0, -1,74, 3,12), V18 (1,74, 0, 3.12), V19 (0, 1,74, -3,12), V20 (0, -1,74, -3,12), V21 (1,74, 0, -3,12), V22 (-1,74, 0, -3,12), V23 (-1,74, -3,12, 0), V24 (1,74, -3,12, 0), V25 (0, -3,12, -1,74), V26 (0, -3,12, 1,74), V27 (0, 3,12, 1,74), V28 (0, 3,12, -1,74), V29 (-1,74, 3,12, 0), V30 (1,74, 3,12, 0), V31 (3,12, -1,74, 0), V32 (3,12, 1,74, 0), V33 (3,12, 0, 1,74), V34 (3,12, 0, -1,74), V35 (-3,12, 1,74, 0), V36 (-3,12, -1,74, 0), V37 (-3,12, 0, -1,74), V38 (-3,12, 0, 1,74). Les bords intermédiaires sont classés comme suit: 1) des bords intermédiaires primaires: sont un ensemble d'arêtes qui sont visibles dans le polyèdre sélectionné, qui peut former un polyèdre régulier convexe. A1 = ensemble d'arêtes primaires, G = nombre d'arêtes secondaires intermédiaires bords primaires A1 = G 2) sont un ensemble de bords qui sont définies à partir d'un sommet intermédiaire primaire à un sommet intermédiaire secondaire. A2 = ensemble des arêtes secondaires, G = nombre d'arêtes primaires, A2 = 2G. 3) tertiaire Arista intermédiaire: sont un ensemble d'arêtes qui sont positionnés entre deux bords secondaires intermédiaires ou intermédiaires entre un premier et un bord de nervure intermédiaire secondaire. A3 = ensemble tertiaire de bords, G = nombre d'arêtes primaires, A3 = 6G).
Il a également trois types de sommets intermédiaires: a) des sommets primaires intermédiaires sont: l'ensemble des sommets intermédiaires sont définies par un ensemble d'arêtes primaires intermédiaires, qui définissent un polyèdre régulier convexe. Le cuboedro triangulaire a (8) huit sommets primaires intermédiaires, qui dans ce cas sont définis par huit triplets cartésiennes. Exemple: V1 (-2,5, 2,5, 2,5), V2 (2,5, 2,5, 2,5), V3 (2,5, -2,5, 2,5), V4 (-2,5, - 2,5, 2,5), V5 (-2,5, 2,5, - 2.5), V6 (-2,5, -2,5, -2,5), V7 (2,5, -2,5, -2,5), V8 (2,5, 2,5, -2,5). Ces huit sommets d'intermédiaires primaires définissent un hexaèdre parfaitement convexe. b) les sommets intermédiaire secondaire est l'ensemble de sommets intermédiaires sont définies par un ensemble d'arêtes secondaires intermédiaires et, dans certains cas, sont définies par un ensemble d'arêtes divers intermédiaires, dont les bords secondaires font partie fondamentale de cet ensemble d'arêtes sundries. Avec l'ensemble des sommets peut toujours secondaire intermédiaire forment un polyèdre régulier convexe. Ces six triplets cartésiennes définissent parfaitement régulière un exemple octaèdre convexe V9 (0, 0, 4), V10 (0, -4, 0), V11 (4, 0,0), V12 (0, 4, 0), V13 (-4, 0.0), V14 (0, 0, -4). c) les sommets tertiaires intermédiaires sont: l'ensemble des sommets intermédiaires sont définis par trois ou plusieurs bords supérieur, qui constituent la qualité de définir un pas régulier convexe de polyèdre. L'ensemble tertiaire de sommets intermédiaires dans certains cas, nous pouvons définir parfaitement l'un des polyèdres archimédiens. Exemple: V15 (0, 1,74, 3,12), V16 (-1,74, 0, 3,12), V17 (0, -1,74, 3,12), V18 (1,74, 0, 3,12), V19 (0, 1,74, -3,12), V20 (0, -1,74, -3,12), V21 (1,74, 0, -3,12), V22 (-1,74, 0, -3,12), V23 (-1,74, -3,12, 0), V24 (1,74, -3,12, 0), V25 (0, -3,12, -1,74), V26 (0, -3,12, 1,74), V27 (0, 3,12, 1,74), V28 (0, 3,12, -1,74), V29 (-1,74, 3,12, 0), V30 (1,74, 3,12, 0), V31 (3,12, -1,74, 0), V32 (3,12, 1,74, 0), V33 (3,12, 0, 1,74), V34 (3,12, 0, -1,74), V35 (-3.12, 1.74, 0), V36 (-3.12, -1.74, 0), V37 (-3.12, 0, -1.74), V38 (-3.12, 0, 1.74). Ces 24 sommets intermédiaires forment parfaitement le polyèdre d'Archimède appelé Octaèdre tronqué. Enviar comentarios Historial Guardadas Comunidad |
| Fecha | |
| Fuente | Trabajo propio |
| Autor | Jose J. Leonard |
https://www.geogebra.org/m/nbxru5tx archive copy at the Wayback Machine https://www.geogebra.org/m/pww32k4a
Licencia
Yo, el titular de los derechos de autor de esta obra, la publico en los términos de la siguiente licencia:
Este archivo está disponible bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Eres libre:
- de compartir – de copiar, distribuir y transmitir el trabajo
- de remezclar – de adaptar el trabajo
- Bajo las siguientes condiciones:
- atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo.
- compartir igual – En caso de mezclar, transformar o modificar este trabajo, deberás distribuir el trabajo resultante bajo la misma licencia o una compatible como el original.
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 00:52 5 ene 2020 | 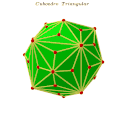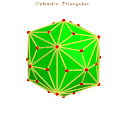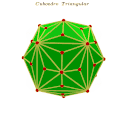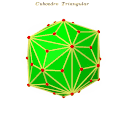| 492 × 480 (2,74 MB) | Jose J. Leonard | User created page with UploadWizard |
Usos del archivo
No hay páginas que enlacen a este archivo.
Uso global del archivo
Las wikis siguientes utilizan este archivo:
- Uso en cv.wikipedia.org
