Semiplano
En geometría euclídea, una línea recta divide un plano en dos semiplanos.[1] Si se agrega la línea recta a uno de los semiplanos, se habla de un semiplano cerrado, mientras que un semiplano sin la línea recta se llama semiplano abierto.
 |
 |
 |
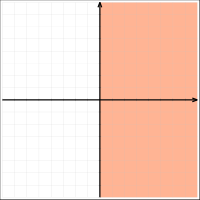 |
Con respecto a los ejes de un sistema de coordenadas cartesianas, existen cuatro semiplanos denominados:
- El semiplano superior, que es el conjunto de puntos con
- El semiplano inferior, que es el conjunto de puntos con
- El semiplano izquierdo, que es el conjunto de puntos con
- El semiplano derecho, que es el conjunto de puntos con
Estas expresiones hacen referencia a semiplanos abiertos. Si en las desigualdades anteriores se sustituye el signo > por el signo ≥, y el signo < por el signo ≤, se obtienen las expresiones de los correspondientes semiplanos cerrados.[2]
Plano complejo editar
Los matemáticos a veces identifican el plano cartesiano con el plano complejo, de forma que el semiplano superior corresponde al conjunto de números complejos con la parte imaginaria positiva:
El término surge de una visualización común del número complejo x + iy como el punto (x, y) en el plano dotado de coordenadas cartesianas. Cuando el eje y está orientado verticalmente, el "semiplano superior" corresponde a la región situada por encima del eje x y, es decir, a los números complejos para los que y > 0.
Es el dominio de muchas funciones de interés en análisis complejo, especialmente en formas modulares.[3] El semiplano inferior, definido por y < 0, es igualmente útil, pero menos utilizado por convención. El disco unidad (el conjunto de todos los números complejos de valor absoluto menor que uno) es equivalente por transformación conforme a (consúltese "métrica de Poincaré"), lo que significa que normalmente es posible realizar los mismos razonamientos en y en
También juega un papel importante en geometría hiperbólica, donde el modelo del semiplano de Poincaré proporciona una forma de examinar el movimiento hiperbólico. La métrica de Poincaré proporciona una métrica hiperbólica en el espacio.[4]
El teorema de uniformización para superficies establece que el semiplano superior es el espacio de recubrimiento universal de superficies con curvatura de Gauss constante negativa.[5]
El semiplano superior cerrado es la unión del semiplano superior y del eje real. Es la clausura del semiplano superior.
Geometría afín editar
Las transformaciones afines del semiplano superior incluyen[6]
- (1) movimientos (x, y) → (x + c, y), c ∈ ℝ, y
- (2) escalados (x, y) → (λ x,λ y), λ > 0.
Proposición: Sean A y B semicírculos en el semiplano superior con centros en el límite. Entonces existe una transformación afín que hace corresponder a A y a B.
- Demostración: Primero, cambiar el centro de A a (0,0). Luego tómese λ = (diámetro de B)/(diámetro de A) y escalar. Luego, trasladar (0,0) al centro de B.
Definición:
- se puede reconocer como el círculo de radio ½ centrado en (½, 0), y como el gráfico en coordenadas polares de
Proposición: (0,0), en y son colineales.
- De hecho, es el reflejo de la línea recta en la circunferencia goniométrica. Así mismo, la diagonal de (0,0) a tiene una longitud al cuadrado de de modo que es el recíproco de esa longitud.
Geometría métrica editar
La distancia entre dos puntos cualesquiera p y q en el semiplano superior se puede definir consistentemente de la siguiente manera: el bisector perpendicular del segmento de p a q se cruza con el límite o es paralelo a él. En el último caso, p y q se encuentran en un rayo perpendicular al límite y se puede utilizar un número positivo para definir una distancia que es invariante sometida a escalado. En el primer caso, p y q se encuentran en un círculo centrado en la intersección de su bisectriz perpendicular y el límite. Según la proposición anterior, este círculo se puede mover mediante un movimiento afín a . Las distancias en se pueden definir utilizando la correspondencia con los puntos en y la medida logarítmica en este rayo. En consecuencia, el semiplano superior se convierte en un espacio métrico.[7] El nombre genérico de este espacio métrico es geometría hiperbólica. En términos de los modelos de geometría hiperbólica, se designa con frecuencia como modelo del semiplano de Poincaré.
Generalizaciones editar
Una generalización natural en geometría diferencial es el n-espacio hiperbólico el conjunto simplemente conexo de dimensión máxima simétrica, n, la variedad de Riemann con constante curvatura seccional −1.[8] Con esta terminología, el semiplano superior es ya que tiene dimensión 2 real.
En teoría de números, la teoría de formas modulares de Hilbert se ocupa del estudio de ciertas funciones sobre el producto directo de n copias del semiplano superior. Otro espacio interesante para los teóricos de los números es el semiespacio superior de Siegel ,[9] que es el dominio de las formas modulares de Siegel.
Véase también editar
Referencias editar
- ↑ Andrés Raya Saro (2021). Álgebra y geometría lineal. Reverte. pp. 25 de 512. ISBN 9788429192926. Consultado el 1 de enero de 2022.
- ↑ Algebra Matematicas 2. Ediciones Umbral. p. 94. ISBN 9789685430029. Consultado el 1 de enero de 2022.
- ↑ Cuatrocientos años de matemáticas en torno al último teorema de Fermat. Editorial Complutense. 1999. pp. 81 de 136. ISBN 9788489784383. Consultado el 1 de enero de 2022.
- ↑ Arlan Ramsay, Robert D. Richtmyer (2013). Introduction to Hyperbolic Geometry. Springer Science & Business Media. pp. 209 de 289. ISBN 9781475755855. Consultado el 1 de enero de 2022.
- ↑ Vialar Thierry (2017). Handbook of Mathematics. BoD - Books on Demand. pp. 241 de 1132. ISBN 9782955199015. Consultado el 1 de enero de 2022.
- ↑ John Milnor (2011). Dynamics in One Complex Variable. (AM-160): (AM-160) - Third Edition. Princeton University Press. pp. 7 de 320. ISBN 9781400835539. Consultado el 1 de enero de 2022.
- ↑ Linda Keen, Nikola Lakic (2007). Hyperbolic Geometry from a Local Viewpoint. Cambridge University Press. pp. 100 de 271. ISBN 9780521682244. Consultado el 1 de enero de 2022.
- ↑ Ben Andrews, Christopher Hopper (2011). The Ricci Flow in Riemannian Geometry: A Complete Proof of the Differentiable 1/4-Pinching Sphere Theorem, Volumen 2011. Springer Science & Business Media. pp. 1 de 296. ISBN 9783642162855. Consultado el 1 de enero de 2022.
- ↑ Serge Lang (2012). Introduction to Algebraic and Abelian Functions. Springer Science & Business Media. pp. 135 de 170. ISBN 9781461257400. Consultado el 1 de enero de 2022.
Enlaces externos editar
- Weisstein, Eric W. «Upper Half-Plane». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.





