Coordenadas esféricas

El sistema de coordenadas esféricas se basa en la misma idea que las coordenadas polares y se utiliza para determinar la posición espacial de un punto mediante una distancia y dos ángulos. En consecuencia, un punto P queda representado por un conjunto de tres magnitudes: el radio $r$, el ángulo polar o colatitud $\theta$ y el azimutal $\varphi$.

Elementos de las coordenadas esféricas

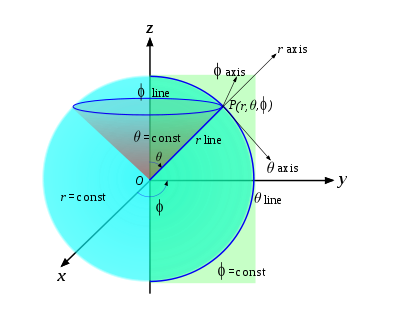
Algunos autores utilizan la latitud, en lugar de colatitud, en cuyo caso su margen es de -90° a 90° (de -π/2 a π/2 radianes), siendo el cero el plano XY. También puede variar la medida del azimutal, según se mida el ángulo en sentido reloj o contrarreloj, y de 0° a 360° (0 a 2π en radianes) o de -180° a +180° (-π a π).

Se debe tener en cuenta qué convención utiliza un autor determinado.

Convenios utilizados

Convenio internacional

La mayoría de los físicos, ingenieros y matemáticos no norteamericanos escriben:

• $\varphi$, el azimutal  : de 0° a 360°
• $\theta$, la colatitud : de 0° a 180°

Esta es la convención que se sigue en este artículo. En el sistema internacional, los rangos de variación de las tres coordenadas son:

$0\leq r<\infty \qquad 0\leq \theta \leq \pi \qquad 0\leq \varphi <2\pi$

La coordenada radial es siempre positiva. Si reduciendo el valor de $r$ llega a alcanzarse el valor 0, a partir de ahí, $r$ vuelve a aumentar, pero $\theta$ pasa a valer π-$\theta$ y $\varphi$ aumenta o disminuye en π radianes. TRP

Convenio estadounidense

Actualmente, el convenio usado en los EE. UU. no es el mismo que el europeo. Para denotar el ángulo azimutal se usa $\theta$ y para referirse al polar, latitud o colatitud se usa $\varphi$.

Relación con otros sistemas de coordenadas

Relación con las coordenadas cartesianas

Sobre los conjuntos abiertos:

$U=\{(r,\theta ,\varphi )|r>0,0<\theta <\pi ,0\leq \varphi <2\pi \}\qquad {\mbox{y}}\qquad V=\{(x,y,z)|x^{2}+y^{2}+z^{2}>0\}$

Existe una correspondencia unívoca $F:V\to U$entre las coordenadas cartesianas y las esféricas, definidas por las relaciones:

$r={\sqrt {x^{2}+y^{2}+z^{2}}}\qquad \theta ={\begin{cases}\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z>0\\{\frac {\pi }{2}}&z=0\\\pi +\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z<0\end{cases}}\qquad \varphi ={\begin{cases}\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y>0{\mbox{ (1° Q)}}\\2\pi +\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y<0{\mbox{ (4° Q)}}\\{\frac {\pi }{2}}{\mbox{sgn}}(y)&x=0\\\pi +\arctan \left({\frac {y}{x}}\right)&x<0{\mbox{ (2° y 3° Q)}}\end{cases}}$

Estas relaciones se hacen singulares cuando tratan de extenderse al propio eje $z\,$, donde $x^{2}+y^{2}=0$, en el cual φ, no está definida. Además, φ no es continua en ningún punto $(x,\ y,\ z)$ tal que $x=0\;$.

La función inversa $F^{-1}$ entre los dos mismos abiertos puede escribirse en términos de las relaciones inversas:

$x=r\operatorname {sen} \,\theta \,\cos \varphi \qquad y=r\operatorname {sen} \,\theta \operatorname {sen} \,\varphi \qquad z=r\,\cos \theta$

Siendo su jacobiano: $\left\vert J\right\vert =r^{2}\operatorname {sen} \theta$

Coordenadas esféricas y ejes cartesianos relacionados

Relación con las coordenadas cilíndricas

Como sistema intermedio entre las coordenadas cartesianas y las esféricas, está el de las coordenadas cilíndricas, que se relaciona con el de las esféricas por las relaciones

$r={\sqrt {\rho ^{2}+z^{2}}}\qquad \theta =\arctan \left({\frac {\rho }{z}}\right)\qquad \varphi =\varphi$

y sus inversas

$\rho =r\,{\operatorname {sen} }\,\theta \qquad \varphi =\varphi \qquad z=r\,\cos \theta$

Líneas y superficies coordenadas

Las líneas coordenadas son aquellas que se obtienen variando una de las coordenadas y manteniendo fijas las otras dos. Para las coordenadas esféricas, estas son:

• Líneas coordenadas $r$: Semirrectas radiales partiendo del origen de coordenadas.
• Líneas coordenadas θ: Semicírculos verticales (meridianos)
• Líneas coordenadas φ: Circunferencias horizontales (paralelos).

Las superficies coordenadas son aquellas que se obtienen fijando sucesivamente cada una de las coordenadas de un punto. Para este sistema son:

• Superficies $r$=cte.: Esferas con centro en el origen de coordenadas.
• Superficies θ=cte.: Conos rectos con vértice en el origen.
• Superficies φ=cte.: Semiplanos verticales.

Las líneas y superficies coordenadas de este sistema son perpendiculares dos a dos en cada punto. Por ello, éste es un sistema ortogonal.

Base coordenada

A partir del sistema de coordenadas esféricas puede definirse una base vectorial en cada punto del espacio, mediante los vectores tangentes a las líneas coordenadas. Esta nueva base puede relacionarse con la base fundamental de las coordenadas cartesianas mediante las relaciones

${\hat {r}}={\operatorname {sen} }\theta \,\cos \varphi \,{\hat {x}}+{\operatorname {sen} }\theta \,{\operatorname {sen} }\,\varphi \,{\hat {y}}+\cos \theta {\hat {z}}$

${\hat {\theta }}=\cos \theta \,\cos \varphi \,{\hat {x}}+\cos \theta \,{\operatorname {sen} }\,\varphi \,{\hat {y}}-{\operatorname {sen} }\theta {\hat {z}}$

${\hat {\varphi }}=-{\operatorname {sen} }\varphi \,{\hat {x}}+\cos \,\varphi \,{\hat {y}}$

e inversamente

${\hat {x}}={\operatorname {sen} }\theta \,\cos \varphi \,{\hat {r}}+\cos \theta \,\cos \varphi \,{\hat {\theta }}-{\operatorname {sen} }\,\varphi \,{\hat {\varphi }}$

${\hat {y}}={\operatorname {sen} }\theta \,{\operatorname {sen} }\,\varphi \,{\hat {r}}+\cos \theta \,{\operatorname {sen} }\,\varphi \,{\hat {\theta }}+\cos \,\varphi \,{\hat {\varphi }}$

${\hat {z}}=\cos \theta \,{\hat {r}}-{\operatorname {sen} }\theta \,{\hat {\theta }}$

En el cálculo de esta base se obtienen los factores de escala

$h_{r}=1\qquad h_{\theta }=r\qquad h_{\varphi }=r\,{\operatorname {sen} }\theta$

Disponiendo de la base de coordenadas esféricas se obtiene que la expresión del vector de posición en estas coordenadas es

${\vec {r}}=r\,{\hat {r}}$

Nótese que no aparecen término en ${\hat {\varphi }}$ o ${\hat {\theta }}$. La dependencia en estas coordenadas está oculta en el vector ${\hat {r}}$.

Diferenciales de línea, superficie y volumen

Diferencial de línea

Un desplazamiento infinitesimal, expresado en coordenadas esféricas, viene dado por

$d{\vec {l}}=h_{r}\,dr\,{\hat {r}}+h_{\theta }\,d\theta \,{\hat {\theta }}+h_{\varphi }\,d\varphi \,{\hat {\varphi }}=dr\,{\hat {r}}+r\,d\theta \,{\hat {\theta }}+r\,{\operatorname {sen} }\,\theta \,d\varphi \,{\hat {\varphi }}$

Diferenciales de área

La expresión general de un diferencial de superficie en coordenadas curvilíneas es complicada. Sin embargo, para el caso de que se trate de una superficie coordenada, $q_{3}={\rm {cte.}}$ el resultado es

$d{\vec {S}}_{q_{3}={\rm {cte}}}=h_{1}\,h_{2}\,dq_{1}\,dq_{2}\,{\hat {q}}_{3}$

y expresiones análogas para las otras dos superficies coordenadas.

En el caso particular de las coordenadas esféricas, los diferenciales de superficie son

• $r$=cte: $d{\vec {S}}_{r={\rm {cte}}}=r^{2}\,{\operatorname {sen} }\theta \,d\theta \,d\varphi \,{\hat {r}}$
• θ=cte: $d{\vec {S}}_{\theta ={\rm {cte}}}=r\,{\operatorname {sen} }\theta \,dr\,d\varphi \,{\hat {\theta }}$
• φ=cte: $d{\vec {S}}_{\varphi ={\rm {cte}}}=r\,dr\,d\theta \,{\hat {\varphi }}$

Diferencial de volumen

El volumen de un elemento en coordenadas curvilíneas equivale al determinante del jacobiano de la transformación, multiplicado por los tres diferenciales. El jacobiano, a su vez, es igual al producto de los tres factores de escala, por lo que

$dV=h_{1}\,h_{2}\,h_{3}\,dq_{1}\,dq_{2}\,dq_{3}$

que para coordenadas esféricas en las que el ángulo vertical empieza en el eje z da

$dV=r^{2}\,{\operatorname {sen} }\,\theta \,dr\,d\theta \,d\varphi$

y en las que el ángulo vertical empieza en el plano XY da

$dV=r^{2}\,{\cos }\,\theta \,dr\,d\theta \,d\varphi$

Operadores diferenciales en coordenadas esféricas

El gradiente, la divergencia, el rotacional y el laplaciano poseen expresiones particulares en coordenadas esféricas. Estas son:

• Gradiente

$\nabla \phi ={\frac {\partial \phi }{\partial r}}{\hat {e}}_{r}+{\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}{\hat {e}}_{\theta }+{\frac {1}{r\,{\operatorname {sen} }\theta }}{\frac {\partial \phi }{\partial \varphi }}{\hat {e}}_{\varphi }$

• Divergencia

$\nabla \cdot {\vec {F}}={\frac {1}{r^{2}}}{\frac {\partial (r^{2}F_{r})}{\partial r}}+{\frac {1}{r\,{\operatorname {sen} }\,\theta }}{\frac {\partial ({\operatorname {sen} }\,\theta \,F_{\theta })}{\partial \theta }}+{\frac {1}{r\,{\operatorname {sen} }\,\theta }}{\frac {\partial (F_{\varphi })}{\partial \varphi }}$

• Rotacional

$\nabla \times {\vec {F}}={\frac {1}{r^{2}{\operatorname {sen} }\,\theta }}\left|{\begin{matrix}{\hat {r}}&r\,{\hat {\theta }}&r\,{\operatorname {sen} }\,\theta \,{\hat {\varphi }}\\&&\\{\frac {\partial }{\partial r}}&{\frac {\partial }{\partial \theta }}&{\frac {\partial }{\partial \varphi }}\\&&\\F_{r}&rF_{\theta }&r{\operatorname {sen} }\,\theta \,F_{\varphi }\end{matrix}}\right|$

• Laplaciano

$\nabla ^{2}\phi ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \phi }{\partial r}}\right)+{\frac {1}{r^{2}\,{\operatorname {sen} }\,\theta }}{\frac {\partial }{\partial \theta }}\left({\operatorname {sen} }\,\theta {\frac {\partial \phi }{\partial \theta }}\right)+{\frac {1}{r^{2}{\operatorname {sen} }^{2}\theta }}{\frac {\partial ^{2}\phi }{\partial \varphi ^{2}}}$

Véase también

• Sistema de coordenadas
• Coordenadas geográficas
• Coordenadas cartesianas
• Coordenadas cilíndricas
• Factores de escala

Referencias

Bibliografía

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 658. ISBN 0-07-043316-X. LCCN 52011515. 
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 177-178. LCCN 55010911. 
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. pp. 174-175. LCCN 59014456. ASIN B0000CKZX7. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 95-96. LCCN 67025285. 
• Moon P, Spencer DE (1988). «Spherical Coordinates (r, θ, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print edición). New York: Springer-Verlag. pp. 24-27 (Table 1.05). ISBN 978-0-387-18430-2. 
• Duffett-Smith P, Zwart J (2011). Practical Astronomy with your Calculator or Spreadsheet, 4th Edition. New York: Cambridge University Press. pp. 34. ISBN 978-0521146548. 

• Datos: Q203218
• Multimedia: Spherical coordinates / Q203218