Distribución t de Student
En probabilidad y estadística, la distribución (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño y la desviación estándar poblacional es desconocida.
| Distribución t de student | ||
|---|---|---|
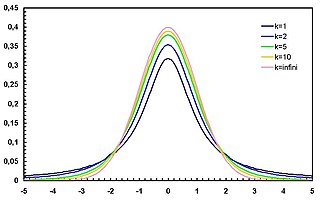 Función de densidad de probabilidad | ||
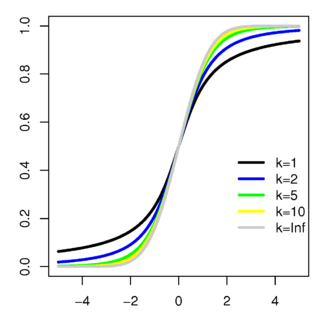 Función de distribución de probabilidad | ||
| Parámetros | grados de libertad (real) | |
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | donde es la función hipergeométrica | |
| Media | para , indefinida para otros valores | |
| Mediana | ||
| Moda | ||
| Varianza | para , indefinida para otros valores | |
| Coeficiente de simetría | para | |
| Curtosis | para | |
| Entropía |
| |
| Función generadora de momentos (mgf) | (No definida) | |
Fue desarrollada por William Sealy Gosset bajo el pseudónimo “Student”.
Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos varianzas muestrales y para la construcción del intervalo de confianza para la diferencia entre las partes de dos poblaciones cuando se desconoce la desviación típica de una población y esta debe ser estimada a partir de los datos de una muestra.
Historia y etimología editar
La distribución de Student fue descrita en el año 1908 por William Sealy Gosset.
En estadística, la distribución t fue derivada por primera vez como distribución posterior en 1876 por Helmert[1][2][3] y Lüroth.[4][5][6] La distribución t también apareció en una forma más general como distribución Pearson Tipo IV en el artículo de Karl Pearson de 1895.[7]
En la literatura en lengua inglesa, la distribución toma su nombre del artículo de William Sealy Gosset de 1908 en Biometrika bajo el seudónimo de "Student".[8] Una versión del origen del seudónimo es que el empleador de Gosset prefería que el personal utilizara seudónimos al publicar artículos científicos en lugar de su nombre real, o prohibía totalmente la publicación de artículos[9], por lo que utilizó el nombre de "Estudiante" para ocultar su identidad. Otra versión es que Guinness no quería que sus competidores supieran que utilizaban la prueba t para determinar la calidad de la materia prima.[10][11]
Gosset trabajó en la fábrica de cerveza Guinness en Dublín, Irlanda, y se interesó por los problemas de las muestras pequeñas, por ejemplo, las propiedades químicas de la cebada, donde el tamaño de las muestras podía ser de sólo 3. El artículo de Gosset se refiere a la distribución como la "distribución de frecuencias de las desviaciones típicas de muestras extraídas de una población normal". Se hizo muy conocida gracias al trabajo de Ronald Fisher, que llamó a la distribución "distribución de Student" y representó el valor de la prueba con la letra t.[12][13]
Distribución t de Student a partir de una muestra aleatoria editar
Sea variables aleatorias independientes distribuidas , esto es, es una muestra aleatoria de tamaño proveniente de una población con distribución normal con media y varianza .
Sean
la media muestral y
la varianza muestral. Entonces, la variable aleatoria
sigue una distribución normal estándar (es decir, una distribución normal con media 0 y varianza 1) y la variable aleatoria
donde ha sido sustituido por , tiene una distribución de student con grados de libertad.
Definición editar
Notación editar
Sean una variable aleatoria continua y , si tiene una distribución con grados de libertad entonces escribiremos o .
Función de densidad editar
La distribución -student tiene como función de densidad
para , donde denota los grados de libertad y es la función gamma.
La expresión anterior también suele escribirse como
donde es la función beta.
En particular, para valores enteros de se tiene que
para par
para impar
Función de distribución editar
La función de distribución puede ser escrita en términos de , la función beta incompleta.
Para
donde
Una fórmula alternativa, válida para es
donde es un caso particular de la función hipergeométrica.
Casos particulares editar
Ciertos valores de dan una forma especial a la función de densidad y de distribución.
- Función de densidad:
- Función de distribución:
- Véase Distribución de Cauchy.
- Función de densidad:
- Función de distribución:
- Función de densidad:
- Función de distribución:
- Función de densidad:
- Véase Distribución normal.
- Función de distribución:
- Véase Función error.
Propiedades editar
Si es una variable aleatoria tal que entonces satisface algunas propiedades.
Media editar
La media de para valores es
Varianza editar
La varianza de para valores es
Curtosis editar
La curtosis de para valores es
Caracterización editar
La distribución de Student con grados de libertad puede definirse como la distribución de la variable aleatoria definida por:
donde
- , es decir, es una variable aleatoria con distribución normal estándar (distribución normal con media 0 y varianza 1).
- , es decir es una variable aleatoria que sigue una distribución chi-cuadrada con grados de libertad.
- y son variables aleatorias independientes.
Para una constante no nula, el cociente
es una variable aleatoria que sigue la distribución no central de Student con parámetro de no-centralidad .
Intervalos de confianza para muestras de la distribución normal editar
Intervalo para la media cuando σ² es desconocida editar
Sean una muestra aleatoria proveniente de una población con distribución donde y son desconocidos.
Se tiene que
y
son independientes entonces el cociente
esto es
Sea tal que
siendo entonces
por lo tanto un intervalo de de confianza para cuando es desconocida es
Distribución t de Student generalizada editar
En términos del parámetro de escala σ̂ editar
La distribución de Student puede generalizarse a 3 parámetros, introduciendo un parámero locacional y un parámetro de escala mediante la relación
o
esto significa que tiene la distribución clásica de Student con grados de libertad.
La resultante distribución de Student no estandarizada tiene por función de densidad:[14]
donde no corresponde a la desviación estándar, esto es, no es la desviación estándar de la distribución escalada , simplemente es parámetro de escala de la distribución.
La distribución puede ser escrita en términos de , el cuadrado del parámetro de escala:
Otras propiedades de esta versión de la distribución son:[14]
En términos del parámetro inverso de escala λ editar
Una parametrización alterna está en términos del parámetro inverso de escala definido mediante la relación . La función de densidad está dada por:[14]
Otras propiedades de esta versión de la distribución son:[14]
Distribuciones relacionadas editar
- Si entonces donde denota la distribución F con y grados de libertad.
Véase también editar
Referencias editar
- ↑ Helmert FR (1875). «Über die Berechnung des wahrscheinlichen Fehlers aus einer endlichen Anzahl wahrer Beobachtungsfehler». Z. Math. U. Physik 20: 300-3.
- ↑ Helmert FR (1876). «Über die Wahrscheinlichkeit der Potenzsummen der Beobachtungsfehler und uber einige damit in Zusammenhang stehende Fragen». Z. Math. Phys. 21: 192-218.
- ↑ Helmert FR (1876). «Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit» [La precisión de la fórmula de Peters para calcular el error de observación probable de observaciones directas de la misma precisión]. Astron. Nachr. (en alemán) 88 (8–9): 113-132. Bibcode:1876AN.....88..113H.
- ↑ Lüroth J (1876). «Vergleichung von zwei Werten des wahrscheinlichen Fehlers». Astron. Nachr. 87 (14): 209-20. Bibcode:1876AN.....87..209L.
- ↑ «Estudios de historia de la probabilidad y la estadística. XLIV. Un precursor de la distribución t.». Biometrika 83 (4): 891-898. 1996. Parámetro desconocido
|vauthors=ignorado (ayuda) - ↑ Sheynin O (1995). «El trabajo de Helmert en la teoría de errores». Arch. Hist. Exact Sci. 49 (1): 73-104. S2CID 121241599. doi:10.1007/BF00374700.
- ↑ Pearson, K. (1 de enero de 1895). «Contribuciones a la teoría matemática de la evolución. II. Skew Variation in Homogeneous Material». Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 186: 343-414 (374). Bibcode:1895RSPTA.186..343P. ISSN 1364-503X. doi:10.1098/rsta.1895.0010.
- ↑ "Student" [William Sealy Gosset] (1908). pdf «El error probable de una media». Biometrika 6 (1): 1-25. JSTOR 2331554. doi:10.1093/biomet/6.1.1. hdl:10338.dmlcz/143545.
- ↑ Walpole, Roland; Myers, Raymond y Ye, Keying (2002). Probability and Statistics for Engineers and Scientists. Pearson Education.
- ↑ Wendl MC (2016). «La fama del seudónimo». Science 351 (6280): 1406. Bibcode:2016Sci...351.1406W. PMID 27013722. doi:10.1126/science.351.6280.1406.
- ↑ Mortimer RG (2005). Matemáticas para la química física (3rd edición). Burlington, MA: Elsevier. pp. 326. ISBN 9780080492889. OCLC 156200058.
- ↑ Fisher RA (1925). «Aplicaciones de la distribución 'de Student'». Metron 5: 90-104. Archivado desde pdf el original el 5 de marzo de 2016.
- ↑ Walpole RE, Myers R, Myers S, Ye K (2006). Probability & Statistics for Engineers & Scientists (7th edición). New Delhi: Pearson. p. 237. ISBN 9788177584042. OCLC 818811849.
- ↑ a b c d Jackman, Simon (2009). Bayesian Analysis for the Social Sciences. Wiley. p. 507.
Enlaces externos editar
- Tabla de distribución de T de Student
- Prueba t de Student en la UPTC de Colombia
- Tabla distribución t de Student
- Distribución t-Student: Puntos porcentuales para probabilidad superior
- Probability, Statistics and Estimation en inglés. Primeros Studentes en la página 112.
- [1] Calcular la probabilidad de una distribución t-Student con R (lenguaje de programación)




![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02732e546784af1fb16d0dc1bb65dd743e2284ad)








![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a24f6de51905e2cbc5b0d4cdae5b1fa7049352)

