Ángulo central

Un ángulo central es un tipo de ángulo cuyo vértice es el centro O de una circunferencia, y cuyos lados son dos radios correspondientes a dos puntos distintos de la circunferencia A y B. Se dice que el ángulo central es subtendido por un arco entre esos dos puntos. La longitud del arco se corresponde con el producto del ángulo central (expresado en radianes) por el radio.^[1] El valor del ángulo central es también conocido como distancia angular del arco.

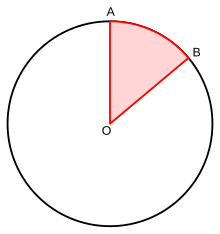
El tamaño de un ángulo central Θ está comprendido entre 0°<Θ<360° о 0<Θ<2π (radianes). Al definir o dibujar un ángulo central, además de especificar los puntos A y B, debe especificarse si el ángulo que se está definiendo es el ángulo convexo (<180°) o el ángulo cóncavo (> 180°). De forma equivalente, se debe especificar si el movimiento del punto A al punto B es dextrógiro o levógiro

Fórmulas editar

Si los puntos de intersección A y B de los lados del ángulo con el círculo forman un diámetro, entonces Θ = 180° es un ángulo llano. (En radianes, Θ = π.)

Sean L el arco menor de la circunferencia entre los puntos A y B; y R el radio de la circunferencia.^[2]

Ángulo Central. Convexo. Es subtendido por el arco menor L

Si el ángulo central Θ es subtendido por L, entonces

$0^{\circ }<\Theta <180^{\circ }\,,\,\,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }={\frac {L}{R}}$

Prueba (para grados): La circunferencia de un círculo de radio R mide 2πR, y el arco menor L es (^Θ/_360°), la parte proporcional de la circunferencia completa (véase arco). Así:

L={\frac {\Theta }{360^{\circ }}}\cdot 2\pi R\,\Rightarrow \,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }.

Ángulo Central. Cóncavo. No es subtendido por L

Prueba (para radianes): La circunferencia de un círculo de radio R is 2πR, y el arco menor L es (^Θ/_2π) la parte proporcional de la circunferencia completa (véase arco). Así:

L={\frac {\Theta }{2\pi }}\cdot 2\pi R\,\Rightarrow \,\Theta ={\frac {L}{R}}.

Si el ángulo central Θ no es subtendido por el arco menor L, entonces Θ es un ángulo de cóncavo y

$180^{\circ }<\Theta <360^{\circ }\,,\,\,\Theta =\left(360-{\frac {180L}{\pi R}}\right)^{\circ }=2\pi -{\frac {L}{R}}$

Sea P el punto de corte de dos rectas tangentes a la circunferencia de centro O en A y en B. Entonces, los ángulos ∠ BOA (convexo) y ∠ BPA son suplementarios (suman 180°).

Ángulo central de un polígono regular editar

Un polígono regular de n lados tiene una circunferencia circunscrita en el que se encuentran todos sus vértices, y su centro es también el centro del polígono. El ángulo central del polígono regular se forma con los radios que unen el centro del polígono con dos vértices consecutivos. La medida de este ángulo es $2\pi /n.$

Véase también editar

Referencias editar

↑ Clapham, C.; Nicholson, J. (2009). «Oxford Concise Dictionary of Mathematics, Central Angle». Addison-Wesley. p. 122. Consultado el Diciembre de 2013.
↑ «Central angle (of a circle)». Math Open Reference. 2009. Consultado el Diciembre de 2013 2013. interactive

Enlaces externos editar

«Central angle (of a circle)». Math Open Reference. 2009. Consultado el Diciembre de 2013. interactive
«Central Angle Theorem». Math Open Reference. 2009. Consultado el Diciembre de 2013. interactive
inscrita y ángulos centrales en un círculo

Datos: Q1094399

[Oxford-1] Clapham, C.; Nicholson, J. (2009). «Oxford Concise Dictionary of Mathematics, Central Angle». Addison-Wesley. p. 122. Consultado el Diciembre de 2013.

[2] «Central angle (of a circle)». Math Open Reference. 2009. Consultado el Diciembre de 2013 2013. interactive

[1]

[2]