Hipérbola

Una hipérbola (del griego ὑπερβολή) es una curva abierta de dos ramas, obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.​ En geometría analítica, una hipérbola es el lugar geométrico de los puntos de un plano, tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.​ Siendo esta constante menor a la distancia entre los focos.

Las asíntotas de la hipérbola se muestran como líneas discontinuas azules que se cortan en el centro de la hipérbola (curvas rojas), C. Los dos puntos focales se denominan F₁ y F₂, la línea negra que une los vértices es el eje transversal. La delgada línea perpendicular en negro que pasa por el centro es el eje conjugado. Las dos líneas gruesas en negro paralelas al eje conjugado (por lo tanto, perpendicular al eje transversal) son las dos directrices, D₁ y D₂. La excentricidad e (e>1), es similar al cociente entre las distancias (en verde) desde un punto P de la hipérbola a uno de los focos y su correspondiente directriz. Los dos vértices se encuentran en el eje transversal a una distancia ±a con respecto al centro.

Etimología

Secciones cónicas.

«Hipérbola» proviene de la palabra griega ὑπερβολή (exceso), y es cognado del término literario «hipérbole».

Historia

Debido a la inclinación del corte, el plano de la hipérbola interseca ambas ramas del cono.

Según la tradición, las secciones cónicas fueron descubiertas por el geómetra y matemático griego Menecmo (380 A. C.- 320 A. C.), en su estudio del problema de la duplicación del cubo,​ mediante el cual demostró la existencia de una solución usando el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por los también geómetras Proclo y Eratóstenes.​

Sin embargo, el primero en usar el vocablo «hipérbola» fue Apolonio de Perge en su tratado Cónicas,​ considerada la obra cumbre sobre el tema de la matemática griega, y donde se desarrolla el estudio de las tangentes a las secciones cónicas.

Ecuaciones de la hipérbola

Ecuaciones canónicas en coordenadas cartesianas

La hipérbola cuyo centro se halla en el origen de coordenadas $O(0,0)\,$es representable mediante una de las siguientes ecuaciones denominadas de manera común como ecuación canónica o forma normal de la ecuación de una hipérbola:

(1)${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1\Rightarrow b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}$

o

(2)${\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1\Rightarrow b^{2}y^{2}-a^{2}x^{2}=a^{2}b^{2}$

En dichas ecuaciones $a$, $b$ y $c$, representan a los semiejes transverso, conjugado y focal, respectivamente. La ecuación (1) representa a las hipérbolas cuyo eje focal es colineal al eje $x$ y la (2) para aquellas que lo son respecto al eje $y$. En la primera ecuación, los focos están en $F(\pm c,0)$ y los vértices en $V(\pm a,0)$. En la segunda, los focos están en $F(0,\pm c)$ y los vértices en $V(0,\pm a)$. En cualquier caso, la relación entre los tres semiejes viene dada por la igualdad:

(3)$c^{2}=a^{2}+b^{2}$

Sin embargo, se debe advertir que, a diferencia del caso de la elipse, no necesariamente $a>b$.

Ecuaciones de una hipérbola con centro en el punto $C(h,k)$

Como en el caso anterior, la ecuación asume una de las siguientes formas:

(4)${\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1$

o

(5)${\frac {(y-k)^{2}}{a^{2}}}-{\frac {(x-h)^{2}}{b^{2}}}=1$

La ecuación (4) corresponde a hipérbolas cuyo eje focal y mayor son paralelos al eje $x$, en las cuales el vértice se halla en $V(h\pm a,k)$ y los focos en $F(h\pm c,k)$. La ecuación (5) es la de las hipérbolas cuyo eje focal y mayor son paralelos respecto al eje $y$ en las cuales los vértices están ubicados en $V(h,k\pm a)$ y los focos en $F(h,k\pm c)$.

Excentricidad

Secciones cónicas.

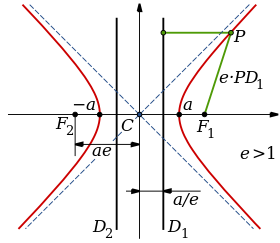
La excentricidad $e$ de una hipérbola es un valor definido como:

$e={\frac {c}{a}}$

donde:

$c$ representa la mitad de la distancia del eje focal.
$a$ representa la mitad de la distancia del eje mayor.

Ya que $c$ es un valor mayor que $a$, la excentricidad de una hipérbola es siempre mayor que 1.

Ecuación general de la hipérbola

La ecuación general de una hipérbola es la siguiente:

(5)$Ax^{2}-Cy^{2}+Dx+Ey+F=0$

Si los coeficientes $A$ y $C$ son de signos diferentes, no nulos y $A>0$ y $C>0$, entonces (5) representa la ecuación general de una hipérbola cuyos ejes son paralelos o colineales a los ejes coordenados o un par de rectas que se cortan.​

Demostración

En la ecuación (5) son separadas las variables en $x$ y $y$ convirtiendo a $A$ y $C$ en factores comunes:

(6)$A\left(x^{2}+{\frac {D}{A}}x\right)-C\left(y^{2}-{\frac {E}{C}}y\right)=-F$

Mediante la completación de cuadrados se reescribe la ecuación anterior como:

(7)$A\left(x^{2}+{\frac {D}{A}}x+{\frac {D^{2}}{4A^{2}}}\right)-C\left(y^{2}-{\frac {E}{C}}y+{\frac {E^{2}}{4C^{2}}}\right)={\frac {D^{2}}{4A}}-{\frac {E^{2}}{4C}}-F$

Ahora se convierten los trinomios de la izquierda en binomios notables:

(8)$A\left(x+{\frac {D}{2A}}\right)^{2}-C\left(y-{\frac {E}{2C}}\right)^{2}={\frac {D^{2}}{4A}}-{\frac {E^{2}}{4C}}-F$

Se convierte el término de la derecha a una constante denominada $t$. De acuerdo al valor de $t$, se presentan los siguientes casos:

1. Si $t>0$, los ejes transverso y focal de la curva son paralelos o colineales al eje $x$.
2. Si $t<0$, los ejes transverso y focal de la curva son paralelos o colineales al eje $y$.
3. Si $t=0$, la ecuación representa a dos rectas que se cortan.

Cualquiera que sea el caso, el centro de la hipérbola o el punto de intersección de las dos rectas es siempre $C\left(-{\frac {D}{2A}},{\frac {E}{2C}}\right)$.

Ecuación de la hipérbola en su forma compleja

Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos $z\,$, en el plano $ReIm\,$; tales que, cualquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distancias $|z-w_{1}|-|z-w_{2}|\,$, a dos puntos fijos llamados focos $w_{1}\,$ y $w_{2}\,$, es una constante positiva igual al doble de la distancia (o sea $2l\,$ ) que existe entre su centro y cualesquiera de sus vértices del eje focal:

$|z-w_{1}|-|z-w_{2}|=2l\,$

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.

Ecuaciones en coordenadas polares

Dos hipérbolas y sus asíntotas en coordenadas cartesianas.

Hipérbola abierta de derecha a izquierda:

$r^{2}=a\sec 2\theta \,$

Hipérbola abierta de arriba abajo:

$r^{2}=-a\sec 2\theta \,$

Hipérbola abierta de noreste a suroeste:

$r^{2}=a\csc 2\theta \,$

Hipérbola abierta de noroeste a sureste:

$r^{2}=-a\csc 2\theta \,$

Hipérbola con origen en el foco derecho:

$r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1-\varepsilon \cos \theta }}$

Hipérbola con origen en el foco izquierdo:

$r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1+\varepsilon \cos \theta }}$

Ecuaciones paramétricas

Hipérbola abierta de derecha a izquierda:

${\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\;\;t\in \,]-\pi /2,\;\pi /2[\,\cup \,]\pi /2,\;3\pi /2[\;\;{\mbox{(un intervalo para cada rama)}}$

o

${\begin{matrix}x=\pm a\sec t+h\\y=b\tan t+k\\\end{matrix}}\;\;t\in \,]-\pi /2,\;\pi /2[\;{\mbox{(un signo para cada rama)}}$

Más manejable es la parametrización

$r(t)=(a\cosh(t),\;\pm b\sinh(t)),\;t\in \,\mathbb {R}$ (un signo para cada rama).

En este caso el vértice en cada rama es $r(0)$ y los puntos $r(t)$ y $r(-t)$ son simétricos respecto al eje focal. En particular podemos graficar una parte de cada rama usando cualquier intervalo: $t\in \,[-s,\;s]$, por ejemplo $t\in \,[-1,\;1]$

Hipérbola abierta de arriba abajo:

${\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}$

También

$r(t)=(a\sinh(t),\;\pm b\cosh(t)),\;t\in \,\mathbb {R}$.

En este caso el vértice en cada rama es $r(0)$ y los puntos $r(t)$ y $r(-t)$ son simétricos respecto al eje focal.

En todas las fórmulas $h$ y $k$ son las abcisa y ordenada, respectivamente, del centro de la hipérbola, $a$ es la longitud del semieje mayor, $b$ es la longitud del semieje menor.

Parámetros focales de la hipérbola y=1/x

Correspondencia entre la hipérbola equilátera $y=1/x$ y su forma focal $x'^{2}/2-y'^{2}/2=1$

Para determinar los parámetros focales de una hipérbola equilátera definida según la ecuación:

$y=1/x$

se puede aplicar una operación matricial que permite modificar las coordenadas de un conjunto de puntos del plano cuando se les aplica un giro $\theta$:

${\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \theta &\operatorname {sen} \theta \\-\operatorname {sen} \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}$

Como la hipérbola equilátera $y=1/x$ está girada con respecto al eje x según un ángulo $\theta =45{\text{°}}$, la matriz de transformación toma la forma:

${\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\-{\sqrt {2}}/2&{\sqrt {2}}/2\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}$

Partiendo de la ecuación de la hipérbola equilátera $y=1/x$, la transformación pasa a ser:

${\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\-{\sqrt {2}}/2&{\sqrt {2}}/2\end{bmatrix}}{\begin{bmatrix}x\\1/x\end{bmatrix}}$

Operando la matriz, resulta:

$x'={\sqrt {2}}/2\,(x+1/x)$

$y'={\sqrt {2}}/2\,(-x+1/x)$

Calculando $x'^{2}-y'^{2}$, se tiene que:

$x'^{2}-y'^{2}=2/4\,[(x^{2}+1/x^{2}+2)-(x^{2}+1/x^{2}-2)]=2$

de donde se deduce que:

$x'^{2}/2-y'^{2}/2=1$

De acuerdo con la notación focal, se tiene que la hipérbola equilátera $y=1/x$ tiene semiejes de valor $a=b={\sqrt {2}}$, y la distancia de sus focos al origen es:

$c={\sqrt {a^{2}+b^{2}}}={\sqrt {2+2}}=2$

Dado que los focos se encuentran en la recta de simetría $y=x$ (inclinada 45°) que corta la hipérbola equilátera $y=1/x$, sus coordenadas proyectadas sobre los ejes son:

$f_{1}=2\,({\sqrt {2}}/2,{\sqrt {2}}/2)=({\sqrt {2}},{\sqrt {2}})$

$f_{2}=2\,(-{\sqrt {2}}/2,-{\sqrt {2}}/2)=(-{\sqrt {2}},-{\sqrt {2}})$

Elementos de la hipérbola

Obtención de una hipérbola mediante la sección de un cono doble.

Eje transversal o transverso

Se le denomina al segmento rectilíneo donde se encuentran los focos y los vértices de la hipérbola. Su valor es $2a$ y es perpendicular al eje conjugado.

Eje conjugado

Es el segmento rectilineo que pasa por el centro de la hipérbola y que es perpendicular o normal al eje transversal y cuya longitud es de $2b$.

Eje focal

Es el segmento rectilineo cuyos extremos son los focos de la hipérbola y cuya longitud es de $2c$. Este eje es colineal con el eje transversal.

Asíntotas

Son las rectas que se intersecan en el centro de la hipérbola y se acercan a las ramas al alejarse estas del centro de la hipérbola. Las ecuaciones de las asíntotas aplicables a las ecuaciones (1) y (2) son, respectivamente:

$\left\{{\begin{array}{llr}y&=&\displaystyle \pm {\frac {b}{a}}x\\\\y&=&\displaystyle \pm {\frac {a}{b}}x\end{array}}\right.$

Las asíntotas de las hipérbolas representadas por las ecuaciones (4) y (5) son expresadas, respectivamente, igualando estas a cero, como sigue:​

$\left\{{\begin{array}{lr}\displaystyle \left({\frac {x-h}{a}}-{\frac {y-k}{b}}\right)\left({\frac {x-h}{a}}+{\frac {y-k}{b}}\right)=0\\\\\displaystyle \left({\frac {y-k}{a}}-{\frac {x-h}{b}}\right)\left({\frac {y-k}{a}}+{\frac {x-h}{b}}\right)=0\end{array}}\right.$

Vértices

Los vértices de una hipérbola son los puntos que son los extremos de su eje transversal. Un vértice es un punto de intersección en el que se encuentran dos o más líneas o segmentos de línea. En matemáticas y geometría, los vértices son elementos fundamentales de las figuras geométricas.

Focos

Son dos puntos, $F_{1}\,y\,F_{2}$, respecto de los cuales permanece constante la diferencia de distancias (en valor absoluto) a cualquier punto, $x$, de dicha hipérbola.

$\vert d(F_{1},x)-d(F_{2},x)\vert =2a$

Centro

Punto medio de los vértices y de los focos de la hipérbola.

Tangentes

La tangente a una hipérbola en cualquier punto de la curva es bisectriz del ángulo formado por los radios vectores de ese punto.

Radio de curvatura

Sea $M(x_{0},y_{0})$ un punto de la hipérbola, entonces el radio de curvatura de la curva es:​

$R=a^{2}b^{2}\left({\frac {x_{0}^{2}}{a^{4}}}+{\frac {y_{0}^{2}}{b^{4}}}\right)^{\frac {3}{2}}={\frac {(r_{1}\cdot r_{2})^{1.5}}{ab}}$

Áreas

Área comprendida entre una rama de hipérbola y una cuerda que la atraviesa

Sea un segmento $AMN$ donde $A$, es el vértice de una rama y $M$ y $N$ son los extremos de una cuerda perpendicular al eje focal, entonces el área es:​

$AMN=x\cdot y-a\cdot b\cdot \ln \left({\frac {x}{a}}+{\frac {y}{b}}\right)=a\cdot b\cdot \cosh ^{-1}\left({\frac {x}{a}}\right)$

Área bajo un arco de hipérbola

Sea un cuadrilátero curvo $OAMG$, formado por los puntos $O$ que es el origen de coordenadas; $A$ que es un vértice; $M(x,y)$ que es un punto de la rama de una hipérbola y $G$ un punto sobre una asíntota, tal que el segmento $MG$ es paralelo a la otra asíntota. El área comprendida por los límites de la figura es:​

$OAMG={\frac {a\cdot b}{4}}+{\frac {a\cdot b}{2}}\cdot \ln \left({\frac {2OG}{c}}\right)$

Trisección angular

Trisección de un ángulo (AOB) usando una hipérbola de excentricidad 2 (curva amarilla)

Como demostró Apolonio de Perge, se puede usar una hipérbola para trisecar un ángulo, un problema de geometría bien estudiado. Dado un ángulo, primero se dibuja un círculo centrado en su vértice O, que interseca los lados del ángulo en los puntos A y B. A continuación, se traza el segmento con los extremos A y B y su bisectriz perpendicular $\ell$. Constrúyase una hipérbola de excentricidad e=2 con $\ell$ como directriz y B como foco. Sea P la intersección (superior) de la hipérbola con el círculo. El ángulo POB triseca el ángulo AOB.

Para probar esto, reflejar el segmento OP sobre la línea $\ell$ para obtener el punto P como la imagen de P. El segmento AP tiene la misma longitud que el segmento BP debido a la reflexión, mientras que el segmento PP tiene la misma longitud que el segmento BP debido a la excentricidad de la hipérbola. Como OA, OP, OP y OB son todos radios del mismo círculo (y por lo tanto, tienen la misma longitud), los triángulos OAP, OPP y OPB son todos congruentes. En consecuencia, el ángulo se ha trisecado, ya que 3×POB=AOB.​

Otras propiedades

Relación de inversión entre la hipérbola y la lemniscata de Bernouilli

• La inversión de una hipérbola equilátera es una lemniscata de Bernouilli y viceversa.
• La lemniscata de Bernouilli es la podaria de una hipérbola equilátera.

Véase también

• Geometría analítica
• Sección cónica
• Recta
• Circunferencia
• Elipse
• Parábola
• Esferas de Dandelin
• Hipérbola unitaria
• Hiperbólico

Bibliografía

• Kazarinoff, Nicholas D. (2003), Ruler and the Round, Mineola, N.Y.: Dover, ISBN 0-486-42515-0 .

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Hipérbola.
• Ejercicios resueltos y video tutoriales sobre hipérbola
• Animación de un plano seccionando un cono y determinando la curva cónica hipérbola
• Apollonius' Derivation of the Hyperbola at Convergence
• Unit hyperbola en PlanetMath.
• Conic section en PlanetMath.
• Conjugate hyperbola en PlanetMath.
• Weisstein, Eric W. «Hipérbola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q165301
• Multimedia: Hyperbolas / Q165301