Primera conjetura de Hardy-Littlewood

En teoría de números, la primera conjetura de Hardy–Littlewood​ muestra una fórmula asintótica para estimar el número de k-tuplas de primos menores que una magnitud dada mediante la generalización del teorema de los números primos. Fue propuesta por primera vez por G. H. Hardy y John Edensor Littlewood en 1923.​

Primera conjetura de Hardy–Littlewood
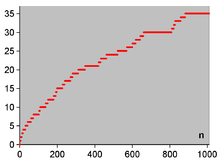Gráfica que muestra la cantidad de números primos gemelos menores que un n dado. La primera conjetura de Hardy–Littlewood predice que hay una infinidad de ellos.
Campo	Teoría de números
Conjeturado por	G. H. Hardy John Edensor Littlewood
Conjeturado en	1923
Problema abierto	Sí

Enunciado

Sean $m_{1},m_{2},\ldots ,m_{k}$ números enteros positivos pares tales que los números de la sucesión $P=(p,p+m_{1},p+m_{2},\ldots ,p+m_{k})$ no forman una clase de residuos completa con respecto a cualquier primo y sea $\pi _{P}(n)$ el número de primos $p$ menores que $n$ siendo todos $p+m_{1},p+m_{2},\ldots ,p+m_{k}$ números primos. Entonces​​

$\pi _{P}(n)\sim C_{P}\int _{2}^{n}{\frac {dt}{\log ^{k+1}t}},$

donde

$C_{P}=2^{k}\prod _{q{\text{ primo,}} \atop q\geq 3}{\frac {1-{\frac {w(q;m_{1},m_{2},\ldots ,m_{k})}{q}}}{\left(1-{\frac {1}{q}}\right)^{k+1}}}$

es un producto sobre los números primos impares y $w(q;m_{1},m_{2},\ldots ,m_{k})$ denota el número de residuos distintos de $m_{1},m_{2},\ldots ,m_{k}$ módulo $q$.

El caso $k=1$ y $m_{1}=2$ es relacionado con la conjetura de los primos gemelos. Específicamente si $\pi _{2}(n)$ denota el número de primos gemelos menores que n, entonces

$\pi _{2}(n)\sim C_{2}\int _{2}^{n}{\frac {dt}{\log ^{2}t}},$

donde

$C_{2}=2\prod _{\textstyle {q{\text{ primo,}} \atop q\geq 3}}\left(1-{\frac {1}{(q-1)^{2}}}\right)\approx 1.320323632\ldots$

es la constante de los primos gemelos.​

Número de Skewes

Los números de Skewes para k-tuplas de primos son una extensión de la definición de número de Skewes para k-tuplas de primos basadas en la primera conjetura de Hardy–Littlewood. El primer primo p que viola la desigualdad de Hardy–Littlewood para la k-tupla P, i.e., tal que

$\pi _{P}(p)>C_{P}\operatorname {li} _{P}(p),$

(si tal primo existe) es el número de Skewes para P.​

Consecuencias

La conjetura se ha mostrado inconsistente con la segunda conjetura de Hardy–Littlewood.​

Generalizaciones

La Conjetura de Bateman-Horn generaliza la primera conjetura de Hardy–Littlewood a polinomios de grado mayor que 1.​

Bibliografía

• Aletheia-Zomlefer, Soren Laing; Fukshansky, Lenny; Garcia, Stephan Ramon (2020). «The Bateman–Horn conjecture: Heuristic, history, and applications». Expositiones Mathematicae 38 (4): 430-479. ISSN 0723-0869. doi:10.1016/j.exmath.2019.04.005. 
• Tóth, László (January 2019). «On the Asymptotic Density of Prime k-tuples and a Conjecture of Hardy and Littlewood». Computational Methods in Science and Technology 25: 143-138. arXiv:1910.02636. doi:10.12921/cmst.2019.0000033. 

• Datos: Q78470924