Teorema de Moore
Un algoritmo que nos sirve para decidir si dos autómatas finitos son equivalentes o no es aquel mencionado en el teorema de Moore, el cual consiste en la elaboración de un árbol que nos ayuda al comparar autómatas distintos. La acción anterior nos permite convertir el problema de la comparación de los lenguajes aceptados en un simple problema de comparación de estados de los autómatas que esperamos comparar.[1]
Explicación (Definición formal) editar
Para poder señalar que 2 estados, q y q’, son compatibles entre sí, ambos deben ser estados finales o ninguno de los dos es un estado final; si esta condición no se cumple, son estados incompatibles. Se puede decir entonces que la idea tras el algoritmo de comparación de dos autómatas finitos determinísticos distintos, se basa en determinar si existe alguna secuencia de caracteres “w”, que al seguirla en ambos autómatas al mismo tiempo no permita llegar a estados incompatibles. Si esta condición se cumple, entonces los autómatas son equivalentes; en caso contrario no son equivalentes.
Debido a que el evaluar todas las cadenas posibles de caracteres en cadenas comunes “w” es sencillamente imposible, debido a que estas son infinitas, se ha pensado en probar todas las distintas combinaciones de estados mediante el uso de un árbol de comparación, el cual para dos autómatas A = (K, ∑, δ, s, F) y A’ = (K’, ∑’, δ’, s’, F’) se elabora de la manera siguiente:
- La “raíz” del árbol generado es el par ordenado (s, s’) que contiene los estados iniciales de A y A’ respectivamente
- Si existiera un par (r, r’) en el árbol, para cada carácter en σ se añaden como “hojas” suyas los pares (rσ, r’σ) donde rσ = δ(r, σ), r’σ = δ(r’, σ), si no estén ya.
- De generarse en el árbol un par (r, r’) de estados incompatibles, se interrumpe la construcción del mismo, concluyendo de esta forma que los dos autómatas no son equivalentes. De no ser así, se continúa a partir del paso número 2.
- En el caso de que no aparezcan nuevos pares (rσ, r’σ) que no se encuentren previamente en el árbol, se termina el proceso, concluyendo que los dos autómatas son equivalentes.
Ejemplo demostrativo editar
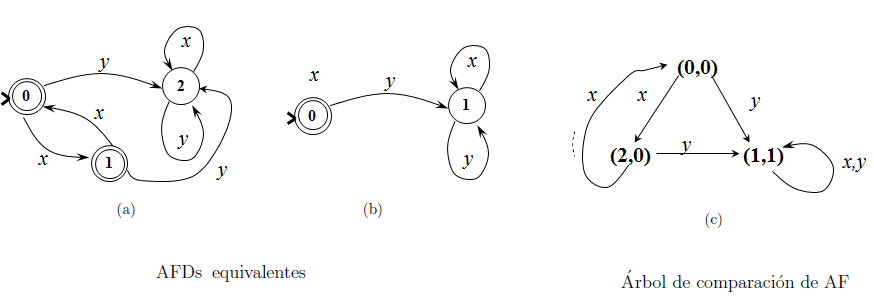
Se dan los autómatas A y A’ de la imagen (A) y (B) respectivamente. Se genera el árbol de comparación se muestra en la imagen. En dicho árbol se muestran adicionalmente, con línea punteada, las ramas que van a nodos ya existentes, como la que va de (q2, r0) a (q0, r0). Por lo cual se concluye que A y A’ son equivalentes.
Sin embargo, en el caso de que los dos autómatas comparados no sean equivalentes, la construcción del árbol de comparación permite encontrar al menos una palabra en que los lenguajes aceptados difieren entre sí. Por ejemplo, los autómatas (a) y (b) de la imagen mostrada. Solo una parte del árbol de comparación se muestra en (c), hasta donde se encuentra el primer par de estados incompatibles. Analizando el árbol de la figura (c), vemos que para llegar desde la raíz del árbol hasta el par incompatible (1,6), hay que gastar los caracteres “x”, “x” y “z”, esto es, la palabra “xxz”. Por lo que podemos llegar a la conclusión de que el autómata (a) no acepta la palabra “xxz”, mientras que el (b) sí la acepta, y por lo tanto sus lenguajes aceptados difieren al menos en la palabra “xxz”.[2]
Comprobación editar
Para probar que este método constituye un algoritmo de decisión para verificar la equivalencia de dos autómatas, hay que mostrar los siguientes puntos:
- El árbol siempre termina, es decir, no se “cicla”.
- Si en el árbol aparecen pares de estados incompatibles (uno final y el otro no final), entonces los lenguajes aceptados por los autómatas son distintos.
- De comparar dos autómatas no equivalentes, entonces en el árbol aparecerán estados incompatibles en algún momento de la evaluación.
El punto 1 se prueba fácilmente porque, los nodos del árbol siendo todos distintos, son un subconjunto de K×K’, que es finito, por lo que el árbol no puede extenderse indefinidamente.
Para probar el punto 2 basta con recorrer en el árbol la trayectoria que lleva al par de estados incompatibles, (r, r’), r ϵ F, r’ !ϵ F’. Simplemente concatenamos los caracteres de entrada σ en dicha trayectoria, y obtendremos una palabra “w” tal que si la aplicamos como entrada al autómata A llegaremos al estado r, es decir, “w” será aceptada. En cambio, si aplicamos la misma w a A’, llegaremos al estado r’, que no es final, por lo que w no será aceptada. Esto muestra que los lenguajes aceptados por A y por A’ difieren en al menos una palabra, “w”.
El punto 3 implica que si no hay pares incompatibles en el árbol, entonces los lenguajes son idénticos. Y, por propiedades de la lógica elemental, al negar la conclusión del punto 3 se obtiene la negación de su premisa en general.[3]