Escala transversal
Una escala transversal o diagonal (en inglès: transversal) es una construcción geométrica usada en un instrumento científico para lograr que una graduación pueda ser leída con un mejor grado de precisión.

Este método se basa en el primer Teorema de Tales. La escala transversal fue usada por diversos autores a lo largo de la historia[1]
Finalmente acabó siendo reemplazada por el nonius que es más versátil y es el que se usa en nuestros días.[2]
Historia
editarLas escalas transversales se utilizaron en un momento en que los instrumentos finamente graduados eran difíciles de construir. Se han encontrado escalas transversales en instrumentos construidos a principios del siglo XIV, se desconoce el inventor, aunque se sabe que Leví ben Gerson las utilizó en su Vara de Jacob.[1][2] (aparentemente inventada el siglo anterior por Jacob ben Makira) y describió el método de la escala transversal aplicado a dicho instrumento.
Thomas Digges atribuyó, erróneamente, el descubrimiento de la escala transversal al navegante y explorador Richard Chancellor (citado por algunos como relojero y con otros nombres como Richard Chansler o Richard Kantzler).[3][4][5][6][7][8] Su uso en instrumentos astronómicos se popularizó a finales del siglo XVI. Tycho Brahe las utilizó y consiguió popularizar la técnica.[9] Finalmente el sistema comenzó a morir una vez el nonius se hizo común a finales del siglo XVIII - más de un siglo después de que Pierre Vernier introdujera la técnica.[10]
En el interim entre las escalas transversales y la escala de Pierre Vernier se utilizó el sistema nonius, desarrollado por Pedro Nunes, que sin embargo, nunca fue de uso común. Tycho Brahe también usó el sistema del nonius, pero parece que fue el único astrónomo prominente que lo usó.
Escala diagonal (transversal rectilínea)
editarPara construir una escala diagonal (transversal recta), se construye una cuadrícula de líneas inmediatamente adyacente a las graduaciones enteras de la escala maestra utilizada. Las líneas verticales se trazan por encima prolongando las graduaciones de dicha escala entera, formando la cuadrícula con "n" líneas horizontales (perpendiculares a las antedichas). La distancia entre las líneas "n" horizontales no es crítica, siempre y cuando sea la misma y exactamente uniforme. Una distancia más grande permite una mayor precisión.
El número de líneas horizontales "n" depende del grado de precisión que el fabricante del instrumento desee proporcionar. Una cuadrícula de cinco líneas horizontales permite la determinación de la medida de una quinta parte de la división de la graduación entera. Una rejilla de diez líneas permite medir décimas.
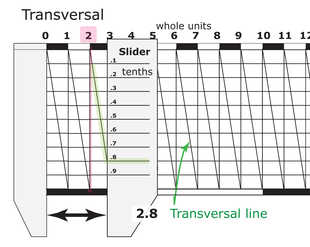
Como se ve en la ilustración, una vez que se ha dibujado la cuadrícula, se trazan las diagonales (escala transversal) en el ejemplo: desde la esquina superior izquierda de una columna de la cuadrícula hasta la esquina inferior opuesta. Esta línea corta las líneas horizontales de la cuadrícula a intervalos iguales. Mediante el uso de un cursor, alidada o indicador de medida, se determina el punto más cercano donde el cursor corta la transversal. La numeración vertical sobre el cursor indica la fracción de división que se está midiendo.
En la ilustración, el cursor se indica mediante la línea vertical. que podría ser el borde de una alidada o un dispositivo similar. Dado que el cursor cruza la transversal más cercana a la sesta línea horizontal de la cuadrícula desde la parte superior, la lectura es 0,6 en la imagen central y 1,8 en la de la derecha.
Siendo a la distancia entre dos unidades consecutivas de la regla y b la separación de la línea superior e inferior, la parte fraccionaria y se puede determinar en función de x medido en la escala transversal:
Tenemos que: a es a b como y es a x, conocido a y b y medido x podemos calcular y.
Dado un número de divisiones de la escala transversal, es el mismo número en el que se divide la unidad de la regla
Por ejemplo para 10 divisiones en la escala transversal, se tienen 10 divisiones de una unidad de la regla.
Escala transversal de arco
editarLas escalas transversales de arco realizan la misma función que las diagonales, pero aplicadas a arcos de circunferencia. En este caso, la construcción de la rejilla es un poco distinta aunque guarda un paralelismo: Un buen símil sería coger una regla de plastilina con las transversales trazadas y doblarla en forma de arco.
Construcción
editarNo puede usar una escala diagonal, hay que crear una rejilla de escalas transversales hecha con secantes de circunferencia comprendidas entre dos grupos de arcos de circunferencia que forman dos limbos graduados. Las secantes se trazan uniendo la división de un limbo con la siguiente, en orden, del otro limbo, y así sucesivamente (ver figura con la ampliación de 2 grados del cuadrante de Tycho Brahe de 2m de radio)[11]
Tycho Brahe
editarTycho Brahe dibujaba, para cada grado, seis transversales de arco de un modo alternado en forma de "V" y cada una de ellas estaba formada por 9 puntos que la dividían en 10 partes, que multiplicadas por 6 dan 60 minutos,[12][9] mientras que Abd al-Mun'im al ‘Âmilî (siglo XVI) las dibujaba todas en el mismo sentido (aunque su instrumento tiene menos precisión).[11]
Arcos transversales
editarEl método de las líneas "transversales rectas" aplicado a las medidas de ángulos sobre limbos circulares o semicirculares en instrumentos astronómicos y geográficos fue tratado por varios autores, estudiando la precisión del sistema. Algunos de ellos indicaban la conveniencia de emplear "arcos transversales", en lugar de las "transversales rectas" clásicas.[13]
Véase también
editarReferencias
editar- ↑ a b Bernard R. Goldstein (6 de diciembre de 2012). The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Springer Science & Business Media. pp. 164-. ISBN 978-1-4613-8569-1.
- ↑ a b Brian Lasater (2008). The Dream of the West, Pt II. Lulu.com. pp. 355-. ISBN 978-1-4303-1382-3.
- ↑ Thomas Digges (1573). Alae seu scalae mathematicae, quibus visibilium remotissima coelorum theatra conscendi, & planetarum omnium itinera nouis & inauditis methodis explorari: ... Thoma Diggeseo, ... authore. pp. 86-.
- ↑ Joseph Needham (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 296-. ISBN 978-0-521-05801-8.
- ↑ Jean Baptiste Joseph Delambre (1819). Histoire de l'astronomie du moyen age; par m. Delambre, chevalier de Saint-Michel et de la Legion-d'honneur ... mme ve Courcier, imprimeur-libraire pour les sciences. pp. 372-.
- ↑ Aimé Laussedat (1898). Recherches sur les instruments: Aperçu historique sur les instruments et les méthodes. La topographie dans tous les temps. Gauthier-Villars.
- ↑ Maurice Daumas (1953). Les Instruments scientifiques aux XVIIe et XVIIIe siècles. Presses Universitaires de France.
- ↑ A.D. Morrison-Low (2 de marzo de 2017). Making Scientific Instruments in the Industrial Revolution. Taylor & Francis. pp. 61-. ISBN 978-1-351-92074-2.
- ↑ a b Tycho Brahe (1946). Tycho Brahe's description of his instruments and scientific work: as given in Astronomiae instauratae mechanica (Wandesburgi 1598). I Kommission hos E. Munksgaard.
- ↑ John Louis Emil Dreyer (13 de febrero de 2014). Tycho Brahe. Cambridge University Press. pp. 58-. ISBN 978-1-108-06871-0.
- ↑ a b The Instruments of Istanbul Observatory (1977). The Instruments of Istanbul Observatory. p. 108.
- ↑ Tycho Brahe (1546-1601). Tychonis Brahe-Astronomiæ instauratæ mechanica. Noribergae, apud L. Hvlsivm, 1602. p. 108.
- ↑ Allain Manesson-Mallet (1702). La Geometrie pratique: Tome second. Contenant la trigoniometrie, ou la mesure des distances par les instrumens geometriques .... chez Anisson directeur de l'Imprimerie Royale. pp. 32-.
Bibliografía
editar- Daumas, Maurice, Instrumentos Científicos del Decimoséptimo y Decimoctavos Siglos y Sus Fabricantes, Portman Libros, Londres 1989 ISBN 978-0-7134-0727-3
Enlaces externos
editar- Wikimedia Commons alberga una categoría multimedia sobre Escala transversal.
- Plantilla con Escala transversal