Media heroniana

En matemáticas, la media heroniana H de dos números reales no negativos A y B se expresa como:​

Un tronco de una pirámide de base cuadrada, con un volumen igual a la altura multiplicada por la media heroniana de las bases cuadradas

$H={\frac {1}{3}}(A+{\sqrt {AB}}+B)\,.$

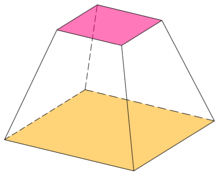
Recibe su nombre de Herón de Alejandría, y se usa para calcular el volumen de un tronco de pirámide o de cono. El volumen es igual al producto de la altura del tronco por la media heroniana de las áreas de las dos caras paralelas que forman sus bases.

La media heroriana de dos números A y B es una media ponderada de su media aritmética y su media geométrica:

$H={\frac {2}{3}}\cdot {\frac {A+B}{2}}+{\frac {1}{3}}\cdot {\sqrt {AB}}\,.$

Aplicación en geometría

La media heroniana se puede utilizar para encontrar el volumen de un tronco de una pirámide o cono. El volumen es igual al producto de la altura del tronco y de la media heroniana de las áreas de las caras paralelas opuestas.

Véase también

• Portal:Matemática. Contenido relacionado con Matemática.
• Media

Bibliografía

• Bullen, P.S. (2003), Handbook of Means and Their Inequalities, Mathematics and Its Applications (2nd edición), Berlin, New York: Springer Science+Business Media, ISBN 978-1-4020-1522-9 .
• Eves, Howard Whitley (1980), Great Moments in Mathematics (Before 1650), Mathematical Association of America, ISBN 978-0-88385-310-8 .

Enlaces externos

• Aplicación de la media heroniana a un problema sobre el volumen de un tronco de cono elíptico

• Datos: Q1187265