Paradoja de Hooper

La paradoja de Hooper es una paradoja falsa^[1] basada en una ilusión óptica. Una forma geométrica con un área de 32 unidades se divide en cuatro partes, que luego se ensamblan en un rectángulo con un área de solo 30 unidades.^[2]

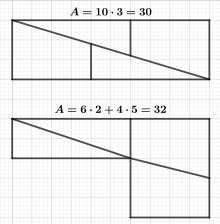
Explicación

Explicación de la paradoja de Hooper. El paralelogramo marrón es el área superpuesta de los dos triángulos.

Tras una inspección minuciosa, uno puede notar que los triángulos de la forma diseccionada no son idénticos a los triángulos en el rectángulo. La longitud del lado más corto en el ángulo recto mide 2 unidades en la forma original pero solo 1.8 unidades en el rectángulo. Esto significa que los triángulos reales de la forma original se superponen en el rectángulo. El área superpuesta es un paralelogramo, cuyas diagonales y lados se pueden calcular mediante el teorema de Pitágoras.

d_{1}={\sqrt {2^{2}+1^{2}}}={\sqrt {5}}

d_{2}={\sqrt {3^{2}+10^{2}}}={\sqrt {109}}

s_{1}={\sqrt {2^{2}+6^{2}}}={\sqrt {40}}

s_{2}={\sqrt {1^{2}+4^{2}}}={\sqrt {17}}

El área de este paralelogramo se puede determinar usando la fórmula de Herón para triángulos. Esto produce:

s={\frac {d_{1}+s_{1}+s_{2}}{2}}={\frac {{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}}}{2}}

para la mitad de la circunferencia del triángulo (la mitad del paralelogramo) y con eso para el área del paralelogramo

{\begin{aligned}F&=2\cdot {\sqrt {s\cdot (s-s_{1})\cdot (s-s_{2})\cdot (s-d_{1})}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot {\sqrt {({\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot (-{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}-{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}+{\sqrt {17}}-{\sqrt {40}})}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot {\sqrt {16}}\\[5pt]&=2\end{aligned}}

.

Entonces, el área superpuesta de los dos triángulos representa exactamente el área desaparecida de 2 unidades.

Historia

William Hooper publicó la paradoja en 1774 en su libro Rational Recreations en el que lo llamó El dinero geométrico. La edición de 1774 de su libro todavía contenía un dibujo falso, que se corrigió en la edición de 1782. Sin embargo, Hooper no fue el primero en publicar esta falacia geométrica, ya que el libro de Hooper era en gran parte una adaptación del libro Nouvelles récréations physiques et mathétiques de Edmé-Gilles Guyot, que había sido publicado en Francia en 1769. La descripción de este libro contiene el mismo dibujo falso que en el libro de Hooper, pero también se corrigió en una edición posterior.

Referencias

↑ W.V. Quine (1976). «The Ways of Paradox and Other Essays». Harvard University Press Cambridge. Consultado el 27 de febrero de 2023.
↑ La Paradoja de Hooper

Enlaces externos

Datos: Q98390306

[1] W.V. Quine (1976). «The Ways of Paradox and Other Essays». Harvard University Press Cambridge. Consultado el 27 de febrero de 2023.

[2] La Paradoja de Hooper

[1]

[2]