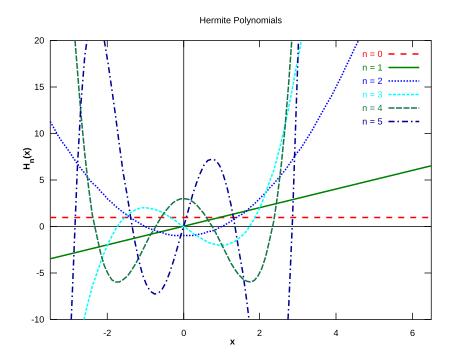
Los polinomios de Hermite se definen como:
H
n
(
x
)
=
(
−
1
)
n
e
x
2
/
2
d
n
d
x
n
e
−
x
2
/
2
{\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}/2}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}/2}\,\!}
(los "polinomios de Hermite probabilísticos" ) o, a veces, como (los "polinomios de Hermite físicos" ):
H
n
p
h
y
s
(
x
)
=
(
−
1
)
n
e
x
2
d
n
d
x
n
e
−
x
2
{\displaystyle H_{n}^{\mathrm {phys} }(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}\,\!}
Estas dos definiciones no son exactamente equivalentes; una es un reescalado trivial de la otra:
H
n
p
h
y
s
(
x
)
=
2
n
/
2
H
n
p
r
o
b
(
2
x
)
{\displaystyle H_{n}^{\mathrm {phys} }(x)=2^{n/2}H_{n}^{\mathrm {prob} }({\sqrt {2}}\,x)\,\!}
Los polinomios físicos pueden expresarse como:
H
n
p
h
y
s
(
x
)
=
(
2
x
)
n
−
n
(
n
−
1
)
1
!
(
2
x
)
n
−
2
+
n
(
n
−
1
)
(
n
−
2
)
(
n
−
3
)
2
!
(
2
x
)
n
−
4
−
…
{\displaystyle H_{n}^{\mathrm {phys} }(x)=(2x)^{n}-{\frac {n(n-1)}{1!}}(2x)^{n-2}+{\frac {n(n-1)(n-2)(n-3)}{2!}}(2x)^{n-4}-\dots }
H
n
{\displaystyle \displaystyle {H_{n}}}
n , con n = 0, 1, 2, 3, .... Estos polinomios son ortogonales con respecto de la función peso (medida )
e
−
x
2
/
2
{\displaystyle e^{-x^{2}/2}\,\!}
o
e
−
x
2
{\displaystyle e^{-x^{2}}\,\!}
es decir
∫
−
∞
∞
H
n
(
x
)
H
m
(
x
)
e
−
x
2
/
2
d
x
{\displaystyle \int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}/2}\,dx}
=
n
!
2
π
δ
n
m
{\displaystyle =n!{\sqrt {2\pi }}~\delta _{\mathit {nm}}}
o
∫
−
∞
∞
H
n
(
x
)
H
m
(
x
)
e
−
x
2
d
x
=
n
!
2
n
π
δ
n
m
{\displaystyle \int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}}\,dx={n!2^{n}}{\sqrt {\pi }}~\delta _{\mathit {nm}}}
donde
δ
n
m
{\displaystyle \delta _{\mathit {nm}}}
delta de Kronecker , que vale la unidad cuando n = m y cero en otro caso. Los polinomios probabilísticos son ortogonales con respecto a la función de densidad de probabilidad normal .
e
2
t
x
−
t
2
=
∑
n
=
0
∞
H
n
p
h
y
s
(
x
)
t
n
n
!
{\displaystyle e^{2tx-t^{2}}=\sum _{n=0}^{\infty }{\frac {H_{n}^{\mathrm {phys} }(x)t^{n}}{n!}}}
editar
Los polinomios de Hermite (en su forma "física") satisfacen las siguientes relaciones de recurrencia :
H
n
+
1
p
h
y
s
(
x
)
=
2
x
H
n
p
h
y
s
(
x
)
−
2
n
H
n
−
1
p
h
y
s
(
x
)
{\displaystyle H_{n+1}^{\mathrm {phys} }(x)=2xH_{n}^{\mathrm {phys} }(x)-2nH_{n-1}^{\mathrm {phys} }(x)}
H
′
n
p
h
y
s
(
x
)
=
2
n
H
n
−
1
p
h
y
s
(
x
)
{\displaystyle {H'}_{n}^{\mathrm {phys} }(x)=2nH_{n-1}^{\mathrm {phys} }(x)}
Una recurrencia integral que se deduce y demuestra en [ 1]
H
e
n
+
1
(
x
)
=
(
n
+
1
)
∫
0
x
H
e
n
(
t
)
d
t
−
H
e
n
′
(
0
)
,
{\displaystyle He_{n+1}(x)=(n+1)\int _{0}^{x}He_{n}(t)dt-He'_{n}(0),}
H
n
+
1
(
x
)
=
2
(
n
+
1
)
∫
0
x
H
n
(
t
)
d
t
−
H
n
′
(
0
)
.
{\displaystyle H_{n+1}(x)=2(n+1)\int _{0}^{x}H_{n}(t)dt-H'_{n}(0).}
A través de estas recurrencias se obtienen los primeros polinomios de Hermite aplicados a la probabilidad son:
H
e
0
(
x
)
=
1
,
H
e
1
(
x
)
=
x
,
H
e
2
(
x
)
=
x
2
−
1
,
H
e
3
(
x
)
=
x
3
−
3
x
,
H
e
4
(
x
)
=
x
4
−
6
x
2
+
3
,
H
e
5
(
x
)
=
x
5
−
10
x
3
+
15
x
,
H
e
6
(
x
)
=
x
6
−
15
x
4
+
45
x
2
−
15
,
H
e
7
(
x
)
=
x
7
−
21
x
5
+
105
x
3
−
105
x
,
H
e
8
(
x
)
=
x
8
−
28
x
6
+
210
x
4
−
420
x
2
+
105
,
H
e
9
(
x
)
=
x
9
−
36
x
7
+
378
x
5
−
1260
x
3
+
945
x
,
H
e
10
(
x
)
=
x
10
−
45
x
8
+
630
x
6
−
3150
x
4
+
4725
x
2
−
945.
{\displaystyle {\begin{aligned}{\mathit {He}}_{0}(x)&=1,\\{\mathit {He}}_{1}(x)&=x,\\{\mathit {He}}_{2}(x)&=x^{2}-1,\\{\mathit {He}}_{3}(x)&=x^{3}-3x,\\{\mathit {He}}_{4}(x)&=x^{4}-6x^{2}+3,\\{\mathit {He}}_{5}(x)&=x^{5}-10x^{3}+15x,\\{\mathit {He}}_{6}(x)&=x^{6}-15x^{4}+45x^{2}-15,\\{\mathit {He}}_{7}(x)&=x^{7}-21x^{5}+105x^{3}-105x,\\{\mathit {He}}_{8}(x)&=x^{8}-28x^{6}+210x^{4}-420x^{2}+105,\\{\mathit {He}}_{9}(x)&=x^{9}-36x^{7}+378x^{5}-1260x^{3}+945x,\\{\mathit {He}}_{10}(x)&=x^{10}-45x^{8}+630x^{6}-3150x^{4}+4725x^{2}-945.\end{aligned}}}
y los primeros polinomios de Hermite aplicados a la física son:
H
0
(
x
)
=
1
,
H
1
(
x
)
=
2
x
,
H
2
(
x
)
=
4
x
2
−
2
,
H
3
(
x
)
=
8
x
3
−
12
x
,
H
4
(
x
)
=
16
x
4
−
48
x
2
+
12
,
H
5
(
x
)
=
32
x
5
−
160
x
3
+
120
x
,
H
6
(
x
)
=
64
x
6
−
480
x
4
+
720
x
2
−
120
,
H
7
(
x
)
=
128
x
7
−
1344
x
5
+
3360
x
3
−
1680
x
,
H
8
(
x
)
=
256
x
8
−
3584
x
6
+
13440
x
4
−
13440
x
2
+
1680
,
H
9
(
x
)
=
512
x
9
−
9216
x
7
+
48384
x
5
−
80640
x
3
+
30240
x
,
H
10
(
x
)
=
1024
x
10
−
23040
x
8
+
161280
x
6
−
403200
x
4
+
302400
x
2
−
30240.
{\displaystyle {\begin{aligned}H_{0}(x)&=1,\\H_{1}(x)&=2x,\\H_{2}(x)&=4x^{2}-2,\\H_{3}(x)&=8x^{3}-12x,\\H_{4}(x)&=16x^{4}-48x^{2}+12,\\H_{5}(x)&=32x^{5}-160x^{3}+120x,\\H_{6}(x)&=64x^{6}-480x^{4}+720x^{2}-120,\\H_{7}(x)&=128x^{7}-1344x^{5}+3360x^{3}-1680x,\\H_{8}(x)&=256x^{8}-3584x^{6}+13440x^{4}-13440x^{2}+1680,\\H_{9}(x)&=512x^{9}-9216x^{7}+48384x^{5}-80640x^{3}+30240x,\\H_{10}(x)&=1024x^{10}-23040x^{8}+161280x^{6}-403200x^{4}+302400x^{2}-30240.\end{aligned}}}
↑ Hurtado Benavides, Miguel Ángel. (2020). De las sumas de potencias a las sucesiones de Appell y su caracterización a través de funcionales. [Tesis de maestría]. Universidad Sergio Arboleda.