Autómata celular de bloque
Un autómata celular de bloque o fraccionado es una clase especial de autómata celular en qué la rejilla de células está dividida entre bloques que no se solapan (con particiones diferentes en pasos de tiempo diferente) y la regla de transición está aplicada a un bloque entero en lugar de a una célula sola. El autómata celular de bloque es útil para simulaciones de cantidades físicas, porque es sencillo elegir reglas de transición que obedezcan restricciones físicas como reversibilidad y leyes de conservación.[1]
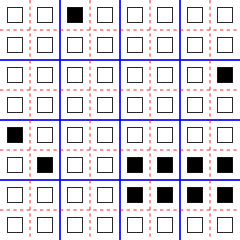
Definición
editarUn autómata celular de bloque consta de los componentes siguientes:[1][2]
- Un enrejado regular de células
- Un conjunto finito de los estados que cada célula puede estar en
- Una partición de las celdas en un teselado uniforme en el que cada mosaico de la partición tiene el mismo tamaño y forma
- Una regla para cambiar la partición después de que cada vez paso
- Una regla de transición, una función que toma como entrada una asignación de estados para las celdas en un único mosaico y produce como salida otra asignación de estados para las mismas celdas.
En cada paso de tiempo, la regla de transición se aplica simultáneamente y sincrónicamente a todos los mosaicos en la partición. Luego, la partición se desplaza y la misma operación se repite en el siguiente paso de tiempo, y así sucesivamente. De esta manera, como con cualquier autómata celular, el patrón de estados celulares cambia con el tiempo para realizar algún cálculo o simulación no trivial.
Vecindad
editarEl esquema de partición más simple es probablemente la vecindad de Margolus, nombrado después de que Norman Margolus, quién fue el primero en estudiar autómata celular de bloque utilizando esta estructura de vecindad. En la vecindad de Margolus, el enrejado está dividido a bloques de 2 células (o 2 × 2 × 2 × 2 cuadrada en dos dimensiones, o 2 2 × 2 × 2 2 2 × 2 2 cubos en tres dimensiones, etc.) cuáles están cambiados por una célula (a lo largo de cada dimensión) encima alternar pasos de tiempo.[1][2][3]
Una técnica estrechamente relacionada debido a K. Morita y M. Harao consiste en particionar cada célula a un número finito de partes, cada parte que es dedicado a algún vecino.[4] La evolución procede por intercambiar las partes correspondientes entre vecinos y entonces aplicando en cada célula una transformación puramente local que depende sólo en el estado de la célula (y no en los estados de sus vecinos). Con tal esquema de construcción, el autómata celular es garantizado para ser reversible si la transformación local es una biyeción. Esta técnica puede ser vista como autómata celular de bloque en un enrejado más bien de células, formados por las partes de cada célula más grande; los bloques de este enrejado más bien se alternan entre los conjuntos de partes dentro de una célula grande sola y los conjuntos de partes en vecinos de células que partes de participación con cada otro.
Véase también
editar- Secuencia de mondadientes, un patrón fractal que puede ser emulado por autómata celular con la vecindad de Margolus
Referencias
editar- ↑ a b c Schiff, Joel L. (2008), «4.2.1 Partitioning Cellular Automata», Cellular Automata: A Discrete View of the World, Wiley, pp. 115-116.
- ↑ a b Toffoli, Tommaso; Margolus, Norman (1987), «II.12 The Margolus neighborhood», Cellular Automata Machines: A New Environment for Modeling, MIT Press, pp. 119-138.
- ↑ Margolus, N. (1984), «Physics-like models of computation», Physica D 10: 81-95, Bibcode:1984PhyD...10...81M, doi:10.1016/0167-2789(84)90252-5.. Reprinted in Wolfram, Stephen, ed. (1986), Theory and Applications of Cellular Automata, Advanced series on complex systems 1, World Scientific, pp. 232-246.
- ↑ Morita, K.; Harao, M. (1989), «Computation universality of 1 dimensional reversible (injective) cellular automata», Transactions Institute of Electronics, Information and Communication Engineers, E 72: 758-762.
Enlaces externos
editar- Critters Simulacro, Seth Koehler, Univ. de Florida