Teorema de Morley
En geometría plana, el teorema de Morley establece que, en un triángulo cualquiera, los tres puntos de intersección entre trisectrices de ángulos adyacentes forman un triángulo equilátero, denominado triángulo de Morley. El teorema fue descubierto en 1889 por el matemático angloestadounidense Frank Morley. Tiene varias generalizaciones, en particular, si se intersecan todas las trisectrices, se obtienen otros cuatro triángulos equiláteros.
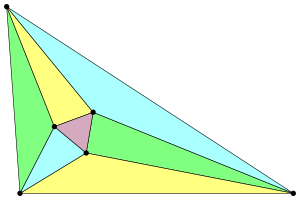
Cabe notar que, como no se puede trisecar un ángulo sólo con regla y compás, no se puede construir el triángulo de Morley con dichas limitaciones. Además, el teorema de Morley no se cumple en las geometrías esférica e hiperbólica[1]
Historia y demostraciones editar
El teorema fue descubierto en 1899 por Frank Morley, quien lo mencionó a sus amigos sin llegar a demostrarlo, es decir, lo dejó como conjetura. Ellos, a su vez, lo difundieron a modo de curiosidad matemática. Finalmente, tras diez años, se publicaron dos demostraciones, una trigonométrica de M. Satyanarayana y otra de geometría elemental de M. T. Naraniengar.[2] Esta última sería redescubierta en 1922 por J. M. Child.[3][4]
Actualmente existen muchas demostraciones matemáticas del teorema de Morley, algunas de las cuales son muy técnicas[5] Entre las demostraciones existentes se encuentra la demostración geométrica de Raoul Bricard en 1922.,[6] la demostración algebraica de Alain Connes[7][8] y la demostración geométrica de John Conway.[9] Esta última demostración empieza con un triángulo equilátero y muestra que se puede construir en torno a él un triángulo semejante a cualquier triángulo dado.
Triángulos de Morley editar
El teorema de Morley conlleva un total de 18 triángulos equiláteros. El triángulo anteriormente descrito en la formulación del teorema, denominado primer triángulo de Morley, tiene sus tres vértices con las siguientes coordenadas trilineales respecto del triángulo original ABC:
- Vértice A = 1 : 2 cos(C/3) : 2 cos(B/3)
- Vértice B = 2 cos(C/3) : 1 : 2 cos(A/3)
- Vértice C = 2 cos(B/3) : 2 cos(A/3) : 1
Otro de los triángulos de Morley que también es triángulo central se denomina segundo triángulo de Morley y viene dado por los siguientes vértices:
- Vértice A = 1 : 2 cos(C/3 − 2π/3) : 2 cos(B/3 − 2π/3)
- Vértice B = 2 cos(C/3 − 2π/3) : 1 : 2 cos(A/3 − 2π/3)
- Vértice C = 2 cos(B/3 − 2π/3) : 2 cos(A/3 − 2π/3) : 1
El tercero de los 18 triángulos equiláteros de Morley que también es central se denomina tercer triángulo de Morley, y viene dado por los siguientes vértices:
- Vértice A = 1 : 2 cos(C/3 − 4π/3) : 2 cos(B/3 − 4π/3)
- Vértice B = 2 cos(C/3 − 4π/3) : 1 : 2 cos(A/3 − 4π/3)
- Vértice C = 2 cos(B/3 − 4π/3) : 2 cos(A/3 − 4π/3) : 1
Los triángulos primero, segundo y tercero de Morley son homotéticos dos a dos. Otro triángulo homotético está formado por los tres puntos X en el circuncírculo del triángulo ABC en el que la recta XX −1 es tangente al cicuncírculo, donde X −1 denota el conjugado isogonal de X. Este triángulo equilátero, denominado triángulo circuntangencial, tiene los siguientes vértices:
- Vértice A = csc(C/3 − B/3) : csc(B/3 + 2C/3) : −csc(C/3 + 2B/3)
- Vértice B = −csc(A/3 + 2C/3) : csc(A/3 − C/3) : csc(C/3 + 2A/3)
- Vértice C = csc(A/3 + 2B/3) : −csc(B/3 + 2A/3) : csc(B/3 − A/3)
Un quinto triángulo, también homotético a los demás, se obtiene al rotar el triángulo circuntangencial π/6 sobre su centro. Este triángulo, el triángulo circunnormal, tiene los siguientes vértices:
- Vértice A = sec(C/3 − B/3) : −sec(B/3 + 2C/3) : −sec(C/3 + 2B/3)
- Vértice B = −sec(A/3 + 2C/3) : sec(A/3 − C/3) : −sec(C/3 + 2A/3)
- Vértice C = −sec(A/3 + 2B/3) : −sec(B/3 + 2A/3) : sec(B/3 − A/3)
Centros de triángulos relacionados editar
El centroide del primer triángulo de Morley viene dado por
- Centro de Morley = X(356) = cos(A/3) + 2 cos(B/3)cos(C/3) : cos(B/3) + 2 cos(C/3)cos(A/3) : cos(C/3) + 2 cos(A/3)cos(B/3)
El primer triángulo de Morley es perspectivo al triángulo ABC, y el perspector es el punto
- Primer centro de Morley-Taylor-Marr = X(357) = sec(A/3) : sec(B/3) : sec(C/3)
Notas y referencias editar
- C. O. Oakley y J. C. Baker, "The Morley trisector theorem," American Mathematical Monthly 85 (1978) 737-745.
- F. Glanville Taylor y W. L. Marr, "The six trisectors of each of the angles of a triangle," Proceedings of the Edinburgh Mathematical Society 33 (1913-14) 119-131.
- ↑ Morley's Theorem in Spherical Geometry, applet Java.
- ↑ H. S. M. Coxeter, «Introduction to Geometry», página 24
- ↑ J. M. Child, «A Proof of Morley's Theorem», The Math. Gaz. (1922), 171
- ↑ Juan M. Conde Calero, «El teorema de Morley» (PDF)
- ↑ Morley's Miracle
- ↑ Richard K. Guy, «The Lighthouse Theorem, Morley & Malfatti - A Budget of Paradoxes», American Mathematical Monthly 114 (2007) 97-141.
- ↑ Alain Connes, «A new proof of Morley's theorem» Archivado el 4 de mayo de 2007 en Wayback Machine., Publications Mathématiques de l'IHÉS, S88 (1998), p. 43-46.
- ↑ Alain Connes, «Symmetries», European Mathematical Society Newsletter No. 54 (Dic. 2004).
- ↑ Demostración de Conway (en inglés)
Enlaces externos editar
En inglés:
- Bogomolny, Alexander. «Morley's Miracle — Several proofs of Morley's theorem». Interactive Mathematics Miscellany and Puzzles (en inglés).
- Morley's Trisection Theorem en MathPages
- Oleksandr Pavlyk. «Morley's Theorem». The Wolfram Demonstrations Project (en inglés). Wolfram Research.
- Richard L. Francis, "Modern Mathematical Milestones: Morley's Mystery", Missouri Journal of Mathematical Sciences, Volume 14:1 (2002), 3 pp.
- Weisstein, Eric W. «Morleys Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
En español:
- «El teorema de Morley» en el blog Gaussianos.