Estereorradián
El estereorradián (símbolo: sr) es la unidad derivada del SI que mide ángulos sólidos[1]. Es el equivalente tridimensional del radián.[2]
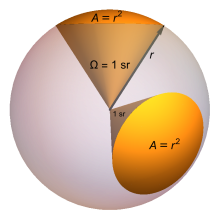

El estereorradián, como el radián, es una unidad adimensional[3][4][5], el cociente del área subtendida y el cuadrado de su distancia al centro. Tanto el numerador como el denominador de esta relación tienen una dimensión de longitud al cuadrado (es decir, L2/L2 = 1, adimensional). Sin embargo, es útil distinguir entre cantidades adimensionales de diferente naturaleza, por lo que el símbolo "sr" se usa para indicar un ángulo sólido. Por ejemplo, la intensidad radiante se puede medir en vatios por estereorradián (W⋅sr−1). El estereorradián era anteriormente una unidad suplementaria del SI, pero esta categoría fue abolida en 1995 y el estereorradián ahora se considera una unidad derivada del SI.[6]
Definición
editarEl estereorradián se define haciendo referencia a una esfera de radio . Si el área de una porción de esta esfera es , un estereorradián es el ángulo sólido comprendido entre esta porción y el centro de la esfera.
Explicación de la definición
editarEl ángulo sólido en estereorradianes es
- ,
donde es la superficie cubierta por el objeto en una esfera imaginaria de radio , cuyo centro coincide con el vértice del ángulo.
Por tanto, un estereorradián es el ángulo que cubre una superficie a una distancia del vértice,
- .
- Analogía con el radián
En dos dimensiones, el ángulo en radianes, está relacionado con la longitud de arco, y es:
- ,
siendo la longitud de arco, y el radio del círculo.
Ángulo de un casquete esférico
editarSi el área es igual a y está dada por el área de un casquete esférico ( ), entonces se cumple que
- .
Por lo tanto, el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a:
- .
Otras propiedades
editarSi A = r2, corresponde al área de un casquete esférico (A = 2π r h) (donde h es la "altura" del casquete) y vale la relación hr = 12π. Por lo tanto, en este caso, un estereorradián corresponde al ángulo plano (o sea en radián) de la sección transversal de un cono simple que comprende el ángulo plano 2θ, con θ correspondiente a :
Este ángulo corresponde al ángulo de apertura plano de 2θ ≈ 1.144 rad or 65.54°.
Un estereorradián también es igual al área esférica de un polígono que tiene un exceso de ángulo de 1 radián, para 14π de una esfera completa, o de [180°π]2
≈ 3282.80635 grados cuadrados.
El ángulo sólido de un cono suya sección transversal define un ángulo 2θ es:
- .
Múltiplos en el Sistema Internacional
editarRespecto a las unidades utilizadas en el Sistema Internacional de Unidades, miliestereorradianes (msr) y microestereoradianes (μsr) se utilizan en forma ocasional para describir los haces de luz y de partículas.[7][8] Otros múltiplos rara vez se utilizan.
Utilización
editarEl estereorradián se utiliza en radiometría[9] y fotometría.[9][10] La intensidad radiante se expresa en vatios por estereorradián[11] y la radiancia, en vatios por metro cuadrado estereorradián.[12]
Ejemplos
editar- La mirada de un ojo humano abarca aproximadamente 2π sr [13]
- Un cono circular, con medio ángulo en el vértice θ, corta en el espacio un ángulo sólido de 2π (1 - cosθ) estereorradiánes. Un ejemplo concreto ilustra la relación entre un ángulo sólido (en el espacio) y el ángulo de vértice correspondiente (ángulo habitual en un plano): Si giramos un ángulo plano (2θ) de 1,144 radianes (65,54°) alrededor de su bisectriz, genera un cono que define un ángulo sólido de 1 estereorradián.
Fórmulas sobre la luz
editarEl lumen es la unidad de flujo luminoso correspondiente al flujo emitido por una fuente con una intensidad luminosa de 1 candela contenida en un ángulo sólido de 1 estereorradián.
Expresiones que contienen el estereorradián:
y
con:
- lm: lumen que es la unidad de flujo luminoso;
- sr: estereorradián que es la unidad de ángulo sólido;
- cd: candela que es la unidad de intensidad luminosa;
- lx: lux que es la unidad de iluminancia de la luz.
Referencias
editar- ↑ «Resolution 8 of the CGPM at its 20th Meeting (1995)». Bureau International des Poids et Mesures. Archivado desde el original el 25 de diciembre de 2018. Consultado el 23 de septiembre de 2014.
- ↑ "Steradian", McGraw-Hill Dictionary of Scientific and Technical Terms, fifth edition, Sybil P. Parker, editor in chief. McGraw-Hill, 1997. ISBN 0-07-052433-5.
- ↑ «1.8 (1.6) quantity of dimension one dimensionless quantity». International vocabulary of metrology — Basic and general concepts and associated terms (VIM). ISO. 2008. Consultado el 22 de marzo de 2011.
- ↑ «SI Brochure: The International System of Units, 9th Edition». International Bureau of Weights and Measures (BIPM). ISBN 978-92-822-2272-0.
- ↑ Mohr, Peter J.; Phillips, William D. (1 de junio de 2015). «Dimensionless units in the SI». Metrologia (en inglés) 52.
- ↑ «Resolution 8 of the CGPM at its 20th Meeting (1995)». Bureau International des Poids et Mesures. Consultado el 23 de septiembre de 2014.
- ↑ Stephen M. Shafroth, James Christopher Austin, Accelerator-based Atomic Physics: Techniques and Applications, 1997, ISBN 1563964848 ISBN 978-1563964848, p. 333
- ↑ R. Bracewell, Govind Swarup, "The Stanford microwave spectroheliograph antenna, a microsteradian pencil beam interferometer" IRE Transactions on Antennas and Propagation 9:1:22-30 (1961)
- ↑ a b BIPM, 2019, chap. 2, section 3, § 2.3.3.
- ↑ BIPM, 2019, chap.2, section 3, § 2.3.4, tableau 4, n. (g).
- ↑ BIPM y 2019, intensité énergétique, chap. 2, section 3, § 2.3.4, tableau 6, s.v..
- ↑ BIPM, 2019, chap. 2, section 3, § 2.3.4, tableau 6, s.v. luminance énergétique.
- ↑ Document sur l'éclairage des bâtiments, LEARN, p. 9 ; véase el artículo « Campo visual ».
Bibliografía
editar- I. Mills, Tomislav Cvitas, Klaus Homann, Nikola Kallay, IUPAC (June 1993). Quantities, Units and Symbols in Physical Chemistry (2nd edición). Blackwell Science Inc. p. 72.
- Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). «Chapter VII. The General Angle [55] Signs and Limitations in Value. Exercise XV.». Escrito en Ann Arbor, Michigan, USA. Trigonometry. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. p. 73. Consultado el 12 de agosto de 2017.
- International Bureau of Weights and Measures (20 de mayo de 2019), The International System of Units (SI) (9th edición), ISBN 978-92-822-2272-0, archivado desde el original el 8 de mayo de 2021.
- Brinsmade, J. B. (December 1936). «Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly». American Journal of Physics 4 (4): 175-179. Bibcode:1936AmJPh...4..175B. doi:10.1119/1.1999110.
- Romain, Jacques E. (July 1962). «Angle as a fourth fundamental quantity». Journal of Research of the National Bureau of Standards, Section B. 66B (3): 97. doi:10.6028/jres.066B.012.
- Eder, W E (January 1982). «A Viewpoint on the Quantity "Plane Angle"». Metrologia 18 (1): 1-12. Bibcode:1982Metro..18....1E. doi:10.1088/0026-1394/18/1/002.