Intersección de conjuntos

En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos partida. Por ejemplo, dado el conjunto de los números pares $P$ y el conjunto de los cuadrados $C$ de números naturales, su intersección es el conjunto de los cuadrados pares.

La intersección de $A$ y $B$ es otro conjunto $A \cap B$ que contiene sólo los elementos que pertenecen tanto a $A$ como a $B$ .

P=\{2,4,6,8,10,\ldots \}

C=\{1,4,9,16,25,\ldots \}

D=\{4,16,36,64,\ldots \}

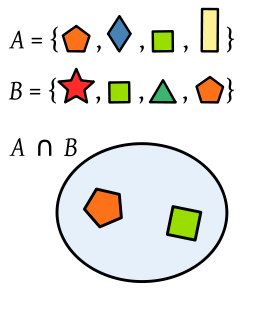
En otras palabras: Cómo, por ejemplo, si A = { a, b, c, d, e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A $\cap$ B = { a, e}

La intersección de conjuntos se denota por el símbolo $\cap$ por lo que $D = P \cap C$ .

Definición editar

La intersección de dos superficies oblicuas.

La intersección de dos superficies perpendiculares.

Intersección de 3 conjuntos (diagrama de Venn).

Intersección de dos conjuntos

A

y

B

.

Dados dos conjuntos $A$ y $B$ , su intersección es otro subconjunto cuyos elementos, necesariamente, pertenecen a ambos conjunto. $A = {π, c, 8, γ, 5, P}$ y $B = {ω, c, 0, Δ, 5, R}$ . Entonces la intersección es $A \cap B = {5, c}$ .

Sean los conjuntos de números naturales $C = {n : n es una potencia de 2}$ y $D = {n : n es un cubo}$ . Su intersección es $C \cap D = {n : n es una potencia de 2 y un cubo} = {n : n es una potencia de 2 cuyo exponente es múltiplo de 3} = {8, 64, 512, ...}$ .

Sean los conjuntos de números pares e impares. Su intersección es el conjunto vacío ∅, ya que no existe ningún número natural que sea par e impar a la vez.

Cuando la intersección de dos conjuntos es vacía, se dice que son disjuntos:

Dos conjuntos $A$ y $B$ se dicen disjuntos si su intersección es el conjunto vacío:

$A\cap B=\varnothing$

Generalizaciones editar

La intersección de un número finito de conjuntos, superior a dos, se define teniendo en cuenta que, debido a la propiedad asociativa (más abajo), el orden en el que se intersequen los conjuntos es irrelevante:

$A_{1}\cap A_{2}\cap \ldots \cap A_{n}=A_{1}\cap (A_{2}\cap (\ldots (A_{n-1}\cap A_{n}){\scriptstyle \ldots })$

La definición más general en teoría de conjuntos se refiere a una familia de conjuntos, un conjunto cuyos elementos son conjuntos a su vez:

Sea $M$ una familia de conjuntos. Su intersección $\cap M$ se define como:

$x\in \bigcap M{\text{ si para cada }}A\in M{\text{ se tiene que }}x\in A$

De este modo, la intersección de un número finito de conjuntos es sólo un caso particular de esta definición general:

A \cap B = \cap M

, donde

M = {A, B}

A 1 \cap ... \cap A n = \cap M

, donde

M = {A 1, ..., A n}

La intersección general de conjuntos se denota de diversas maneras:v

$\bigcap M=\bigcap _{A\in M}A=\bigcap _{i\in I}A_{i}{\text{ ,}}$

donde esta última se aplica en el caso de que utilicemos un conjunto índice, definiendo $M$ como ${A i : i \in I}$ .

Propiedades editar

Artículo principal: Álgebra de conjuntos

De la definición de intersección puede deducirse directamente:

Idempotencia. La intersección de un conjunto $A$ consigo mismo es el propio $A$ :

$A\cap A=A$

La intersección de $A$ y $B$ es un subconjunto de ambos:

$A\cap B\subseteq A,B$

La intersección de un conjunto $B$ con un conjunto $A$ que lo contenga, deja a $B$ inalterado:

$B\subseteq A\rightarrow A\cap B=B$

La intersección de conjuntos poseen también propiedades similares a las operaciones con números:

Propiedad asociativa. La intersección de los conjuntos $A$ y $B \cap C$ es igual a la intersección de los conjuntos $A \cap B y C$ :

$(A\cap B)\cap C=A\cap (B\cap C)$

Propiedad conmutativa. La intersección de los conjuntos $A$ y $B$ es igual a la intersección de los conjuntos $B$ y $A$ :

$A\cap B=B\cap A$

Elemento absorbente. La intersección de un conjunto $A$ con el conjunto vacío $\emptyset$ es $\emptyset$ :

$A\cap \varnothing =\varnothing$

Todas estas propiedades se deducen de propiedades análogas para la conjunción lógica.

En relación con la operación de unión existen unas leyes distributivas:

Propiedad distributiva

$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ , y por tanto:
$A \cup (A \cap B) = A$

$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ , y por tanto:
$A \cap (A \cup B) = A$

Se cumple que ∅ ⊂ A∩B∩C ⊂ A∩B ⊂ A ⊂ A∪B ⊂ A∪B∪C ⊂ Ω donde Ω es el conjunto universal.^[1]

Teoría axiomática editar

En las teorías axiomáticas de conjuntos usuales, como ZFC o NBG, la existencia de la intersección de una familia de conjuntos no se postula de manera independiente, sino que se demuestra como consecuencia del esquema axiomático de reemplazo.

Véase también editar

Referencias editar

↑ Rojo. Álgebra I

Literatura del tema editar

Dorronsoro, José; Hernández, Eugenio (1996). Números, grupos y anillos. Addison-Wesley/Universidad Autónoma de Madrid. ISBN 84-7829-009-5.
Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.

Yu. M. Korshunov. Fundamentos matemáticos de la cibernética. Editorial Mir, Moscú s/f.

Datos: Q185837
Multimedia: Intersection (set theory) / Q185837

[1] Rojo. Álgebra I

[1]