Wikipedia

Mecanobiología

ciencia multidisciplinar que se ocupa del comportamiento de las células cuando son sometidas a cargas mecánicas
Este artículo o sección necesita ser wikificado, por favor, edítalo para que cumpla con las convenciones de estilo.
Este aviso fue puesto el 29 de octubre de 2023.

La mecanobiología celular (mecano que deriva de mecánica, bios que significa vida, y -logía, que significa estudio) es una ciencia multidisciplinar que se ocupa del comportamiento de las células cuando son sometidas a cargas mecánicas y las diversas respuestas y mecanismos de transducción que llevan a cabo.[1]​[2]​

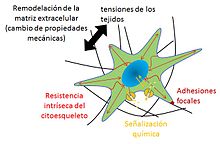
Mecanobiología
Esquema interacciones mecanoquímicas de la célula.

Las cargas mecánicas modulan morfológica y estructuralmente los tejidos vivos, induciendo en ellos cambios en su composición, y en sus funciones. Estos cambios se deben a alteraciones en la matriz extracelular, causadas por las células, las cuales son capaces de sentir fuerzas mecánicas y convertirlas en respuestas biológicas.[3]​ Mecanobiología se define como el estudio de los mecanismos mediante los cuales las células son capaces de detectar y responder a estímulos mecánicos, la importancia de esta disciplina multidisciplinar radica en que dichos estímulos juegan un papel muy importante en la diferenciación y desarrollo celular debido a que la carga mecánica que experimentan las células afecta a la proliferación celular y a los genes de la matriz extracelular, pudiendo provocar de esta manera alteraciones fisiológicas y patológicas.

Esta ciencia se originó a partir de la comprensión del efecto de las cargas mecánicas en la remodelación ósea. Es por eso, que el principio de mecanobiología y el análisis de su importancia en cuanto a la diferenciación celular durante la remodelación ósea sirve de precedente para generalizar esta ciencia. Por lo tanto, sus primeros pasos se basaron en la Ley de Wolff (1892) que como principio dice que el hueso tiende a optimizar su estructura con un tamaño mínimo para una máxima resistencia.[4]​

La mecanobiología es abordada tanto desde un punto de vista experimental como teórico. La aproximación experimental conlleva la aplicación de cargas y estímulos mecánicos a los tejidos y células, y la observación directa de los efectos; mientras que la llamada Mecanobiología Computacional intenta determinar las reglas cuantitativas que gobiernan los efectos mecánicos de la diferenciación, crecimiento y adaptación celular, dependiendo de la geometría y de las propiedades de los materiales.[5]​

La finalidad de la mecanobiología celular es definir los estímulos mecánicos que producen una reacción u otra sobre las células, es decir, determinar cuál es el estímulo encargado de desencadenar cada una de las posibles respuestas biológicas celulares específicas. Estas respuestas biológicas son procesos como la diferenciación celular, el crecimiento celular, la remodelación tisular o su mantenimiento.

El estudio de las propiedades mecánicas de las células se puede realizar por medio de micro manipulación. Las técnicas de micro-manipulación incluyen microscopía de fuerza atómica, técnicas ópticas, como el uso de pinzas ópticas, aspiración con micropipeta, técnicas acústicas, de flujo, micropilares y microscopía de fuerza por tracción, técnicas magnéticas y métodos de simulación computacional.

Microscopía de fuerza atómica(AFM)

editar

La microscopía de fuerza atómica, también conocida como Atomic Force Microscopy (AFM) en inglés, es una técnica óptica capaz de caracterizar superficies nanométricas, con magnitudes inferiores al límite óptico de difracción. Además proporciona mayor resolución que otras técnicas como: pinzas ópticas, técnicas magnéticas o la micropipeta.

En 1986, Binnig et al.[6]​ introdujo un nuevo tipo de microscopio que era capaz de estudiar las superficies de materiales aislantes a escala a atómica.

Modos de empleo/uso

editar

La técnica se basa en la medida de la interacción atómica, entre la punta y la superficie de la muestra. El valor de la fuerza de interacción es de µN a nN, esta depende de la distancia de la punta (normalmente de silicio o nitruro de silicio) y la superficie.

A medida que el piezoeléctrico escanea los ejes horizontales, la palanca (cantiléver) que sostiene la punta se flexiona arriba o abajo en eje vertical. Siguiendo la ley de Hooke, esta deflexión se detecta mediante un láser, que incide sobre un fotodetector, que se encarga de seguir la evolución de la sonda del microscopio.

Figura 1. Instrumentación AFM

En esta técnica se usan tres modos que se muestran a continuación:[7]​

  1. Modo de contacto En este modo la punta se encuentra en contacto con la muestra en todo momento. La fuerza que se ejerce con la aguja es constante y se pueden detectar movimientos verticales de la punta del cantiléver inferiores a los Angstrom. Se pueden medir muchos tipos de muestras, además de obtener la información de su elasticidad. En cambio, al tener la punta continuamente en contacto con la superficie es más fácil que esta se desgaste o se deteriore. Hay diversas propiedades mecánicas a nano-escala que se pueden determinar gracias a este modo como por ejemplo el módulo elástico, la fuerza, la adhesión o la fricción[8]​
  2. Modo de no-contacto Consiste en hacer vibrar al cantiléver cerca de la zona de la superficie a una distancia de entre 10 a 100 Å(Angstrom). Se utiliza para muestras en las que no se quiere dañar su superficie. Como principales ventajas está la posibilidad de medir diferentes gradientes de fuerzas en la muestra y la no contaminación ni deterioro de estas. Como desventajas, la obtención de una resolución menor.
  3. Modo de contacto intermitente (“tapping mode”) Con la intención de solucionar el problema de desgaste de la superficie de la muestra por la punta, se utiliza este modo. El contacto de la punta con la superficie es intermitente a lo largo del barrido. La señal se obtiene midiendo la amplitud que genera la amortiguación de la punta sobre la superficie.

Aplicaciones biomédicas:

Esta técnica ha sido utilizada no solamente para la caracterización de la topografía de diversos materiales, sino también para el estudio de la mecánica de diferentes sistemas biológicos.

Uno de los estudios se ha realizado en linfocitos. Hu et al. (2009),[9]​ presentaron un estudio de la arquitectura de la membrana celular de los linfocitos y su respuesta mecánica en tres estadios del ciclo de la vida de la célula: reposo, activación o tras experimentar muerte celular programada (apoptosis).

Otro estudio ha sido realizado por Daniel Navajas et al (2016)[10]​ para medir la mecánica de la ECM (matriz extracelular) en la escala en la que las células investigan las características mecánicas de su microambiente.

Aspiración con micropipeta

editar

La aspiración con micropipeta es una técnica experimental que permite el estudio del comportamiento mecánico de las células de forma individual y su interacción mecánica con el entorno.[11]​ Con el mismo objetivo destacan también otros procedimientos como la microscopia de fuerza atómica (AFM), la citometría óptica, etc.

En esta técnica se genera una fuerza de succión que provoca una deformación en la superficie de la célula mediante su extensión hacia el interior de la micropipeta. Posteriormente, se analiza la longitud aspirada para conocer el comportamiento de la célula y calcular los parámetros elásticos y viscoelásticos que la caracterizan.[12]​ Otra aplicación novedosa de esta técnica es la caracterización de la adhesión celular[13]​.
Es una de las menos exigentes para implementar en un laboratorio, además de ser una técnica muy extendida y aceptada en bibliografía. Por el contrario, presenta algunas desventajas como que las medidas son más complicadas y requieren procesado de imagen digital posterior.

Análisis datos obtenidos experimentalmente

editar

Las deformaciones sufridas por las células son del orden de los μm y las fuerzas necesarias para deformarlas varían entre 10 pN y 1 nN según la rigidez de las mismas. Es por esto que las tensiones y presiones medidas serán del orden de los pN/μm2 o nN/ μm2 (equivale a Pa o kPa, respectivamente).[14]​

La fuerza (F) a la que se somete una célula estática en la micropipeta viene dada por el producto de la presión de succión y el área transversal de la micropipeta, ecuación (1). Sin embargo, la célula puede estar en movimiento debido al estiramiento de las microvellosidades; en este caso la fuerza viene determinada por la ecuación (2).[15]​

 
Figura 1. Esquema de la realización del ensayo de aspiración con micropipeta. ∆P presión de succión. Rp radio de la micropipeta. Rc radio de la célula. Lp longitud de la célula aspirada.
  (1)
  (2)

Donde Ut es la velocidad de unión y Uf es la velocidad de movimiento libre. El resto de los parámetros quedan reflejados en la figura 1 de la realización del ensayo.

La tensión superficial que sufre la membrana celular durante la aspiración puede explicarse mediante la Ley de Laplace para una esfera de pared delgada. Si consideramos que la longitud aspirada es igual al radio de la micropipeta (punto crítico), la tensión superficial queda determinada por la ecuación (3).[14]​

  (3)

Donde Patm es la presión atmosférica, Pp es la presión en el interior de la micropipeta y N es la ley de Laplace para una esfera de pared delgada (ej.: valores experimentales en neutrófilos N~35 [N/m]).[12]​

Modelos de comportamiento

editar

Los modelos de comportamiento de esta técnica vienen determinados por la linealidad entre el cociente   y la presión de succión aplicada (∆P). Esto permite determinar si la célula se encuentra en un estado sólido o líquido.

Para valores inferiores al punto crítico   , relación esférica o semiesférica), se observa una relación lineal puesto que la célula se deformará a volumen constante. Por encima de este valor crítico (  ) se puede distinguir:

 
Figura 2. Gráfica de posibles comportamientos de la célula en la aspiración con micropipeta
  • Líquido: Se tiene un comportamiento como líquido si la célula fluye al interior de la micropipeta. Esto es debido a que el radio de la célula fuera de la pipeta disminuye mientras que su recíproco aumenta. Este comportamiento se observa en células como los neutrófilos.[14]​
  • Sólido: Las células no se introducirán en la micropipeta y seguirán un comportamiento lineal por encima del punto crítico comportándose como sólido elástico debido a la rigidez de corte de la membrana que le otorga una resistencia a la cizalladura.[14]​ Algunas de estas células son los condrocitos, eritrocitos o células endoteliales.[16]​

Modelos de simulación para el procesado de datos

editar

Para la simulación de esta técnica se han desarrollado modelos numéricos axisimétricos de elementos finitos donde se tiene en cuenta, el contacto de la célula con la micropipeta y la no linealidad intrínseca del problema, para poder determinar tanto el módulo de elasticidad como la relación de Poisson.[11]​

Estos modelos pueden implementarse en tecnologías futuras para la medición automática de propiedades mecánicas de células, basándose en esta técnica y también en el tránsito celular a través de constricciones de flujo[11]​.

 
Figura 3. Modelo axisimetrico. Célula deformada por la aspiración de la micropipeta. Simulación realizada por el software ABAQUS

Estos modelos pueden implementarse en futuras tecnologías para la medición automática de propiedades mecánicas de células. El problema mecánico y la no linealidad de la estructura requiere el uso de técnicas de elementos finitos, así como un proceso iterativo de cálculo para simular la carga de la célula. Se simula la micropipeta como una superficie rígida donde se produce el contacto con la célula. El contacto entre la célula esférica y la superficie del microcapilar se supone sin fricción.[11]​

En la figura 3 se puede ver un ejemplo de la aplicación de un modelo axisimétrico con algunas aproximaciones donde se aprecia la célula deformada.

Técnicas ópticas

editar

Técnicas eléctricas en Mecanobiología Celular

editar

El uso de técnicas eléctricas se encuentra ampliamente desarrollado y son dos los campos en que más se está investigando: desarrollo de sensores basados en sistemas microelectromecánicos (MEMS) y aplicación de campos eléctricos para estimulación celular. Sistemas microelectromecánicos (MEMS)

Las fuerzas ejercidas por las células juegan un papel vital en procesos tan variados como la migración, la diferenciación o la apoptosis. El estudio de las propiedades mecánicas de células individuales es esencial para poder entender la relación entre la capacidad de las células de sentir y producir fuerzas y su función. En las últimas décadas se han desarrollado dispositivos basados en MEMS para caracterizar las propiedades mecánicas de las células, así como las fuerzas que ejercen. Los MEMS presentan unas dimensiones por debajo de 1 milímetro y constan de elementos cuyo tamaño oscila entre 1 y 100 micrómetros. De forma general, presentan una unidad central que procesa la información (microprocesador) y varios componentes que interaccionan con el entorno (microsensores). Una de las características principales de los MEMS es que, al trabajar en la escala micrométrica, la superficie específica (relación área superficial/volumen) de las muestras es muy elevada. Como consecuencia, los efectos de superficie, incluyendo las fuerzas electromagnéticas (cargas eléctricas y momentos magnéticos), predominan sobre los efectos volumétricos.

Se denominan Bio-MEMS a los sistemas MEMS aplicados al ámbito de la medicina y salud. La evolución de estos sistemas ha beneficiado en gran medida al campo del diagnóstico. A continuación, se van a presentar algunas de las principales aplicaciones de estos dispositivos, como son el estudio de fuerzas de tracción y contracción, rigidez de las células y su citoesqueleto.

  • Estudios de fuerzas de tracción. A finales de los años 90, se desarrollaron dispositivos capaces de medir tracciones subcelulares permitiendo que pequeñas regiones de fibroblastos ejercieran fuerzas sobre micropalancas calibradas. Estos estudios permitieron cuantificar las fuerzas generadas por pequeños contactos adhesivos y demostraron que la fuerza ejercida por la célula no era continua. El análisis de las fuerzas ejercidas por las distintas regiones de las células permitió comprender mejor el mecanismo de migración celular[17]​
  • Estudios de rigidez celular. El desarrollo de sensores para el estudio de la mecanobiología continuó con el desarrollo de dispositivos capaces de caracterizar aspectos como la rigidez de las células y su citoesqueleto. Para ello fue necesario implementar la tecnología que permitiera la aplicación y medida de grandes deformaciones y fuerzas, reproduciendo la respuesta celular a daños y grandes esfuerzos[18]​[19]​
  • En relación con la respuesta celular al daño, cabría destacar el desarrollo de una micropalanca microfabricada con un biopolímero capaz de medir la fuerza de contractilidad ejercida por cardiomiocitos. Este dispositivo, diseñado inicialmente para el estudio de la función y disfunción cardiacas, se puede utilizar para el estudio de otros tejidos.[20]​

Un área de gran interés científico y tecnológico es el desarrollo de sensores in vivo para la monitorización continua de la salud humana. Los beneficios del uso de MEMS con este fin es su gran rendimiento, elevada sensibilidad, rapidez de respuesta, control temporal, tamaño y coste.[21]​ Continuando en este ámbito, habría que destacar los dispositivos Micro TotalAnalysis, que automatizan e integran todos los procesos necesarios para el análisis químico de una muestra y que pueden aparecer integrados en dispositivos médicos, incluyendo los stents[22]​ o implantes cocleares.

Estimulación por campos eléctricos

Las células son entes vivos con una gran capacidad de adaptación. El control celular no depende únicamente de la propia célula, sino que señales externas también pueden producir cambios. La estimulación eléctrica se vale de dicho mecanismo, siendo posible inducir tanto su muerte (apoptosis) como su proliferación. También es posible inducir un desplazamiento de la célula e inducir su diferenciación.

 
Posibles efectos de la estimulación eléctrica de una célula

Las células utilizan impulsos eléctricos como un medio de señalización. A pesar de que no se conocen en detalle los mecanismos, es conocido que los campos eléctricos son capaces de alterar, entre otros, la producción de ATP.[23]​ Una disminución en la disponibilidad de energía produce alteraciones en el citoesqueleto,[24]​ lo cual deriva, entre otros, en alteraciones mecánicas de la célula.

Estos impulsos eléctricos son generados debido a gradientes iónicos y participan en el control de diversos procesos de proliferación, diferenciación y apoptosis, así como el control de la forma celular, tanto en células madre como en aquellas más diferenciadas[25]​

Dado que el control no depende únicamente del impulso generado por la propia célula, sino que es susceptible al ambiente eléctrico próximo, el uso de campos eléctricos permite múltiples posibilidades, como el estudio de propiedades celulares, la elaboración de nuevas terapias o la mejora de las técnicas de proliferación in vitro entre otros. El potencial de membrana ha demostrado ser un aspecto clave en la generación de tumores y la regeneración de tejidos, siendo posible el uso de campos eléctricos para dirigir la diferenciación de dichas células.[26]​ Además de factores como la diferenciación y proliferación, numerosos estudios han revelado el efecto de la estimulación eléctrica sobre la migración celular.[27]​ El uso de campos eléctricos ha demostrado ser una técnica in vitro novedosa capaz de dirigir la diferenciación de células madre hacia diversos tipos celulares como osteocitos, cardiomiocitos o neuronas. Actualmente se continúan caracterizando los mecanismos de interpretación de las señales eléctricas por parte de las células, con el objetivo de poder definir los parámetros adecuados para su uso en ingeniería de tejidos.

Técnicas acústicas

editar

Las técnicas acústicas aplicadas al estudio de las propiedades de la célula se basan en el empleo de ondas de sonido para la manipulación de células tanto de manera individual como colectiva. Permiten obtener desde medidas de adhesión celular y de interacción célula-superficie, hasta algunos parámetros mecánicos. Se trata de técnicas muy novedosas, todavía en proceso de desarrollo gracias a las distintas ventajas que presentan: son técnicas no invasivas, ya que las ondas acústicas pueden penetrar el objeto diana/la célula sin dañarlo, sencillas y baratas, que se pueden aplicar a una o varias células sin necesidad de pretratamientos.[28]​ Uno de los instrumentos más utilizados es el microscopio de ultrasonidos.

En cuanto a la mecánica celular, el microscopio de ultrasonidos permite obtener el módulo de compresibilidad y la densidad, así como distintos parámetros acústicos que caracterizan a la célula. Es una de las pocas técnicas que puede estudiar las propiedades mecánicas del interior de una célula. Su funcionamiento se basa en la reflexión de ultrasonidos en las interfaces de la célula.

Para llevar a cabo el ensayo, la célula se apoya en un sustrato y se rodea de un medio conductor que permita el paso de los ultrasonidos con la menor atenuación posible, como se puede ver en la Figura 1. El sustrato suele ser una placa de Petri y el medio conductor agua o medio de cultivo. Se envía una onda de ultrasonidos perpendicular a la célula y se recogen las ondas reflejadas: por un lado, el eco producido por la superficie de contacto entre la célula y el medio y, por otro, el reflejado en la interfaz célula-sustrato. De esta manera, se puede obtener directamente el espesor de la célula. A partir de esta medida, se calculan la velocidad del sonido en la célula, su impedancia acústica y coeficiente de atenuación. Una vez conocidos estos parámetros, se puede caracterizar mecánicamente la célula: su densidad y su módulo de compresibilidad.

Cálculo de los parámetros acústicos y mecánicos

editar

Los parámetros acústicos que se pueden calcular son: la velocidad del sonido en el medio celular, el coeficiente de atenuación de los ultrasonidos y la impedancia acústica de la célula. Por su parte, los parámetros mecánicos serán la densidad, el espesor y el módulo de compresibilidad.[29]​

Las señales S0, S1 y S2 se reflejan desde el sustrato y de la superficie superior e inferior de la célula, respectivamente. Si estas tres señales se pueden separar en el dominio del tiempo, los parámetros se calcularán en función de este. Sin embargo, si la separación temporal no es posible, el cálculo se realizará en el dominio de la frecuencia. A continuación, se muestran los cálculos en el dominio temporal.

En primer lugar, se puede obtener de manera directa el espesor (e) de la célula como:

  (1)

donde c0 es la velocidad del sonido en el medio conductor, t0 y t1 son los tiempos de llegada de las señales S0 y S1, respectivamente.

Esto permite calcular la velocidad del sonido en la célula (cc), a partir de la siguiente ecuación:

  (2)

Con estos parámetros, se puede obtener la impedancia acústica de la célula (ZC) y su coeficiente de atenuación.

Una vez se tienen todos los parámetros acústicos necesarios, se procede a calcular los mecánicos. La densidad de la célula (ρc) se obtiene de la siguiente manera:

  (3)

El módulo de rigidez a cortante (GC) y el módulo de compresibilidad (KC) se pueden relacionar con la densidad y la velocidad del sonido a través de la siguiente ecuación:

  (4)

La célula se puede aproximar como fluido, por lo tanto, el módulo de rigidez a cortante es mucho menor en comparación con el módulo de compresibilidad. Por ello, se elimina este término de la ecuación, quedando:

  (5)

Otros usos

editar

La información sobre las propiedades mecánicas de la célula que se obtienen con esta técnica permite, por ejemplo, diferenciar las células apoptóticas (células que tienen una muerte programada) de las no apoptóticas, basándose en las diferencias de espesor y atenuación.[30]​

Además de la obtención de parámetros mecánicos y acústicos para la caracterización de diferentes tipos celulares, esta técnica acústica permite también la obtención de imágenes. Siguiendo el funcionamiento de los ultrasonidos, se obtiene una imagen en escala de grises en función de la intensidad de las ondas de presión reflejadas y recogidas por el transductor. De esta manera, se consiguen diferenciar las principales estructuras celulares: membrana, núcleo y nucleolo.[30]​

Dispositivos microfluídicos

editar

Son los que dan una orden a ciertos elementos que pueden cambiar su comportamiento ante un estímulo. Un ejemplo: un sistema de riego. se podría considerar un medio de fluido, pero el dispositivo que activa el riego; podría asociarse a un control o máquina predeterminada.

Flujo paralelo al sustrato

editar

Micropilares

editar

Microscopía de fuerza por tracción (TFM)

editar

Técnicas magnéticas

editar

Uno de los métodos para la caracterización de las propiedades mecánicas de las células se basa en la micromanipulación magnética. Consiste en el empleo de partículas magnéticas que son adheridas a la superficie de la célula que se quiere estudiar. Posteriormente, se aplica un campo magnético externo que desplace dichas partículas, pudiendo determinar sus propiedades mediante el empleo de pinzas magnéticas.

Las pinzas magnéticas son un instrumento científico empleado para la caracterización y manipulación de las células mediante el empleo de fuerzas y momentos de fuerza. La fuerza magnética resultante depende tanto de las propiedades del material y del tamaño de la partícula como del gradiente de dicho campo magnético, el cual puede ser generado empleando varias configuraciones.[31]​[32]​[33]​

Para la realización de la técnica, uno de los extremos de la célula se une a una superficie mientras que el extremo libre se une a una partícula magnética. Estas uniones se suponen específicas a los extremos de la célula y que son capaces de soportar fuerzas sin afectar a las propiedades mecánicas y biológicas (véase Ilustración 1). Las pinzas magnéticas consisten en un par de imanes colocados encima de un soporte de muestras de un microscopio invertido, el cual está equipado con una cámara CCD conectada a un digitalizador de vídeo que captura el desplazamiento y rotación obtenidos. Estas pinzas son capaces de ejercer fuerzas superiores a 1 nN, y pueden ser empleadas para manipular e incluso rotar partículas magnéticas entre 0.5-5 μm. Las fuerzas son posteriormente cuantificadas con un análisis de las fluctuaciones laterales de la biomolécula en la dirección perpendicular a la fuerza aplicada.[34]​

Estos campos magnéticos son generados con imanes permanentes móviles o con electroimanes. Mediante un único imán se puede lograr una fuerza atractiva en la partícula magnética, pero es necesario un mínimo de dos para generar una rotación, obteniendo además un gradiente magnético constante y el consecuente campo magnético homogéneo. Se trata de una técnica manejable que permite generar campos magnéticos que varíen con el tiempo.

Esta técnica posee una serie de ventajas e inconvenientes respecto a otras como el AFM o las ópticas:

Una de las ventajas de estas técnicas es la capacidad de las pinzas magnéticas de generar tanto fuerzas lineales como de torsión en la partícula. Además, al tratarse de manipulación magnética, se evita que se produzcan daños en las células como ocurre con el láser de las pinzas ópticas, por ejemplo. Por otro lado, esta técnica permite trabajar en un amplio rango de frecuencias y la realización de varias medidas simultáneamente. Por último, la instrumentación empleada es menos compleja con una implementación más sencilla, con un coste más bajo, en contraste con técnicas como el AFM o las pinzas ópticas.[35]​

Sin embargo, a pesar de sus numerosas ventajas, las pinzas magnéticas no son tan versátiles como pueden ser otras técnicas como las pinzas ópticas o el AFM, debido a que la configuración del imán no es tan manejable. Por otro lado, los momentos aplicados son tan elevados que impiden que se pueda medir directamente la rotación generada. Además, el amplio rango de frecuencias y la sensibilidad que nos otorga la técnica es limitada por la detección del vídeo, no permitiendo que se puedan tomar desplazamientos muy pequeños o muy rápidos. Por último, para producir campos magnéticos altos o un gradiente magnético se requieren altas corrientes en los electroimanes, lo que puede producir calentamientos o polos inducidos que provocan variaciones en el campo aplicado dando lugar a una alteración en la fuerza constante aplicada, perdiendo una de las ventajas de esta técnica.

Un ejemplo en el que se emplea esta técnica es en el MTC (Magnetic twisting citometry), una herramienta capaz de analizar la transmisión de fuerzas a través de la membrana celular y calcular la rigidez celular y sus variaciones. Esta técnica consiste en inducir una tensión local de torsión en micropartículas magnéticas unidas a los receptores de membrana, mediante ligandos en los receptores celulares específicos, con el fin de medir las rotaciones producidas. La rotación de la partícula provoca que se generen tensiones mecánicas en la célula que se oponen a dicha rotación en la zona de unión con la misma. Así, midiendo el momento aplicado y la rotación de la partícula se puede deducir las propiedades mecánicas de la célula.[36]​[37]​

Otra aplicación del magnetismo en la mecanobiología celular es el inducir estímulos, mecánicos o de estrés, permitiendo el estudio de las señalizaciones que estos provocan en la célula.[38]​[39]​ Además, se pueden emplear campos magnéticos prolongados en el tiempo para inducir diferenciación celular selectiva con un elevado grado de precisión.[40]​[41]​[42]​

Compresión

editar

Simulación computacional: Método Continuos

editar

Simulación computacional: Métodos Discretos

editar

Para modelar las diferentes interacciones dentro del entorno celular (célula-célula o célula-matriz, por ejemplo) se pueden utilizar herramientas de simulación computacional mediante métodos discretos, continuos o continuo-discretos (también llamados híbridos).

Este análisis computacional se puede utilizar cuando ocurra alguna de las siguientes situaciones:[43]​

  1. La cantidad de datos sea demasiado grande como para desarrollar una análisis manual
  2. La reproducibilidad del análisis sea importante
  3. La dinámica del sistema no pueda ser entendida intuitivamente
  4. La escala temporal del experimento sea muy larga
  5. Los elementos de interés no sean observables o controlables experimentalmente
  6. Los experimentos conlleven implicaciones éticas

Simulación computacional: métodos discretos

Este tipo de método utiliza modelos de matemáticas discretas para simular la posición de un elemento biológico en distintos tiempos y las interacciones de ese elemento con su entorno biológico. Para ello, dicho elemento biológico se representa con una variable discreta, esto es, es almacenado como un objeto individual dentro de la simulación. Los métodos discretos se pueden clasificar como deterministas (sin componente aleatoria) o estocásticos (cuyas interacciones dependen del azar).

La principal característica de un modelo computacional discreto es que permite describir elementos a escala subcelular (proteínas, filamentos de actina...), de manera cuantitativa y mostrando la evolución temporal de los diferentes tipos de moléculas. La desventaja es que para llevar a cabo dicha simulación se requiere un alto coste computacional.[44]​

Para desarrollar un modelo con métodos discretos se puede partir o no de imágenes tomadas en laboratorio o de un conjunto de datos experimentales que sirvan para establecer el modelo. Una vez que el modelo ha sido formulado, para lo cual pueden utilizarse distintos tipos de aproximaciones matemáticas (ecuaciones diferenciales lineales o no lineales, matriz de Leslie…), se lleva a cabo la simulación. Por último, hace falta validar el modelo, ya que la simulación no es exacta. Esto se debe a que no estamos resolviendo el modelo de manera general, sino para unos puntos predefinidos del espacio y/o tiempo; por lo tanto, la solución que nos proporcione esta simulación será una solución particular del modelo. Para validar esta simulación se lleva a cabo un mayor número de iteraciones, de modo que si el error disminuye con cada nueva iteración, podemos concluir que la simulación converge. De este modo queda verificado el modelo.

Aunque el modelo no nos proporcione una solución general, nos sirve para entender el comportamiento de lo que estamos simulando. Así, por ejemplo, nos permite ver qué sucedería ante distintas situaciones y cómo varían de una a otra según modifiquemos el valor de los parámetros. Por ello, los modelos discretos son muy utilizados en biología celular.

Las células biológicas están constantemente expuestas a tensiones mecánicas. En respuesta a estas tensiones, las células pueden cambiar su forma, migrar, adherirse al sustrato o cambiar su estado de otra manera (dividirse, morir, etc). Modelar estos fenómenos no es una tarea trivial debido a la complejidad biológica y a las diversas escalas implicadas. Para esta tarea, investigadores de diversas áreas (ingeniería, matemáticas, física, biología…) desarrollaron modelos basados en agentes para entender la dinámica de los tejidos según la actuación de las células. En estos modelos las células son consideradas como unidades separadas (por tanto, discretas) y se puede simular sus evoluciones dinámicas a lo largo del tiempo.

Se han desarrollado varios métodos para imitar a las células en el espacio. Podemos dividirlos en dos grandes familias: métodos que se basan en cuadrículas o redes y métodos que no utilizan cuadrículas para modelar las células en el espacio. Ambos permiten modelar el crecimiento, la migración, la división y la muerte celular.

 
Figura 1. Representación de los varios tipos de modelos con cuadrícula. A) Un cuadrado ocupado por muchas células. B) Un cuadrado ocupado por una sola célula. C) Una célula ocupando varios cuadrados.

En los modelos con cuadrícula (figura 1), un cuadradito puede estar ocupado por varias células, lo que permite modelar una gran población celular (tipo A); estar ocupado por una única célula (tipo B), lo cual se consigue, por ejemplo, mediante triangulación de Delaunay y diagramas de Voronoi; o una única célula puede ocupar varios cuadrados (tipo C). Este último modelo se conoce como modelo celular de Potts (Cellular Potts Model). Cada uno de estos tres métodos permite describir el efecto de las fuerzas mecánicas de una célula sobre su entorno o sobre un grupo de células vecinas. Existe también un cuarto método, llamado LGCA (Lattice Gas Celular Automaton), en el cual se añade una variable “velocidad”. Generalmente contiene varias células en un mismo cuadrado.[45]​

 
Figura 2.

En los modelos sin cuadrícula (figura 2) podemos distinguir los modelos basados en un centro (center-based models) y los modelos de célula deformable (deformable cell models). Los primeros modelan las interacciones entre las células basándose en las fuerzas o energías entre los centros de las células, bajo la hipótesis de que la trayectoria que sigue cada célula en el espacio puede ser descrita mediante una ecuación de movimiento; aunque tienen la desventaja de que no permiten representar de manera aleatoria la forma de las células. Los segundos permiten representar formas complejas de células con muchos detalles, proporcionando resultados a nivel subcelular de fuerzas de tracción, compresión o cizalladura, entre otros. Además, también permiten incorporar modelos de adhesión específica (e.g. fuerza electroestática) y no específica (e.g. debido a las proteínas).[45]​

A continuación se enumeran algunos ejemplos concretos que pueden ser encontrados en la literatura:

  • Modelado de crecimiento de tumores, invasión y angiogénesis, donde se usan ecuaciones diferenciales no lineales que consideran la componente celular como discreta.[46]​
  • Modelado del comportamiento mecánico de los filamentos de actina presentes en los filopodios para entender el desplazamiento celular y la adhesión célula-matriz,[44]​ utilizando la ecuación de Langevin.
  • Modelado de la matriz extracelular para conocer la interacción de las fibras de colágeno con los fibroblastos durante el proceso de regeneración de un tejido.[47]​ Los fibroblastos son tratados como objetos discretos cuyos caminos vienen dados por ecuaciones diferenciales ordinarias y afectan al modelo de manera estrictamente local, dada la baja densidad de estas células durante la regeneración

Referencias

editar
  1. ↑ Jansen, Karin A.; Donato, Dominique M.; Balcioglu, Hayri E.; Schmidt, Thomas; Danen, Erik H. J.; Koenderink, Gijsje H. (Noviembre de 2015). «A guide to mechanobiology: Where biology and physics meet». Biochimica Et Biophysica Acta 1853 (11 Pt B): 3043-3052. ISSN 0006-3002. PMID 25997671. doi:10.1016/j.bbamcr.2015.05.007. Consultado el 29 de octubre de 2023. 
  2. ↑ Köster, Sarah; Janshoff, Andreas (Noviembre de 2015). «Editorial - Special issue on mechanobiology». Biochimica Et Biophysica Acta 1853 (11 Pt B): 2975-2976. ISSN 0006-3002. PMID 26247339. doi:10.1016/j.bbamcr.2015.08.002. Consultado el 29 de octubre de 2023. 
  3. ↑ Wang, J. H.-C.; Thampatty, B. P. (Marzo de 2006). «An introductory review of cell mechanobiology». Biomechanics and Modeling in Mechanobiology 5 (1): 1-16. ISSN 1617-7959. PMID 16489478. doi:10.1007/s10237-005-0012-z. Consultado el 29 de octubre de 2023. 
  4. ↑ Delgado-Calle, J.; Riancho, J. A. (Marzo de 2013). «Mecanobiología celular y molecular del tejido óseo». Revista de Osteoporosis y Metabolismo Mineral 5 (1): 51-56. ISSN 1889-836X. doi:10.4321/S1889-836X2013000100009. Consultado el 29 de octubre de 2023. 
  5. ↑ van der Meulen, Marjolein C. H.; Huiskes, Rik (Abril de 2002). «Why mechanobiology? A survey article». Journal of Biomechanics 35 (4): 401-414. ISSN 0021-9290. PMID 11934410. doi:10.1016/s0021-9290(01)00184-1. Consultado el 29 de octubre de 2023. 
  6. ↑ Binnig, G.; Quate, C. F.; Gerber, C. (3 de marzo de 1986). «Atomic force microscope». Physical Review Letters 56 (9): 930-933. ISSN 1079-7114. PMID 10033323. doi:10.1103/PhysRevLett.56.930. Consultado el 29 de octubre de 2023. 
  7. ↑ Frewin, C. (7 de marzo de 2012). Atomic Force Microscopy Investigations into Biology - From Cell to Protein. InTech. ISBN 978-953-51-0114-7. doi:10.5772/2092. Consultado el 29 de octubre de 2023. 
  8. ↑ Haase, Kristina; Pelling, Andrew E. (6 de marzo de 2015). «Investigating cell mechanics with atomic force microscopy». Journal of the Royal Society, Interface 12 (104): 20140970. ISSN 1742-5662. PMC 4345470. PMID 25589563. doi:10.1098/rsif.2014.0970. Consultado el 29 de octubre de 2023. 
  9. ↑ Haase, Kristina; Pelling, Andrew E. (6 de marzo de 2015). «Investigating cell mechanics with atomic force microscopy». Journal of the Royal Society, Interface 12 (104): 20140970. ISSN 1742-5662. PMC 4345470. PMID 25589563. doi:10.1098/rsif.2014.0970. Consultado el 29 de octubre de 2023. 
  10. ↑ Jorba, Ignasi; Uriarte, Juan J.; Campillo, Noelia; Farré, Ramon; Navajas, Daniel (Enero de 2017). «Probing Micromechanical Properties of the Extracellular Matrix of Soft Tissues by Atomic Force Microscopy». Journal of Cellular Physiology 232 (1): 19-26. ISSN 1097-4652. PMID 27163411. doi:10.1002/jcp.25420. Consultado el 29 de octubre de 2023. 
  11. ↑ a b c d Esteban-Manzanares, Gustavo; González-Bermúdez, Blanca; Cruces, Julia; De la Fuente, Mónica; Li, Qingxuan; Guinea, Gustavo V.; Pérez-Rigueiro, José; Elices, Manuel et al. (Mayo de 2017). «Improved Measurement of Elastic Properties of Cells by Micropipette Aspiration and Its Application to Lymphocytes». Annals of Biomedical Engineering 45 (5): 1375-1385. ISSN 1573-9686. PMID 28097526. doi:10.1007/s10439-017-1795-7. Consultado el 29 de octubre de 2023. 
  12. ↑ a b Evans, E.; Yeung, A. (Julio de 1989). «Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration». Biophysical Journal 56 (1): 151-160. ISSN 0006-3495. PMC 1280460. PMID 2752085. doi:10.1016/S0006-3495(89)82660-8. Consultado el 29 de octubre de 2023. 
  13. ↑ Hogan, Brenna; Babataheri, Avin; Hwang, Yongyun; Barakat, Abdul I.; Husson, Julien (21 de julio de 2015). «Characterizing cell adhesion by using micropipette aspiration». Biophysical Journal 109 (2): 209-219. ISSN 1542-0086. PMC 4621874. PMID 26200857. doi:10.1016/j.bpj.2015.06.015. Consultado el 29 de octubre de 2023. 
  14. ↑ a b c d Hochmuth, R. M. (Enero de 2000). «Micropipette aspiration of living cells». Journal of Biomechanics 33 (1): 15-22. ISSN 0021-9290. PMID 10609514. doi:10.1016/s0021-9290(99)00175-x. Consultado el 29 de octubre de 2023. 
  15. ↑ Shao, J. Y.; Hochmuth, R. M. (Noviembre de 1996). «Micropipette suction for measuring piconewton forces of adhesion and tether formation from neutrophil membranes». Biophysical Journal 71 (5): 2892-2901. ISSN 0006-3495. PMC 1233775. PMID 8913626. doi:10.1016/S0006-3495(96)79486-9. Consultado el 29 de octubre de 2023. 
  16. ↑ Discher, D. E.; Boal, D. H.; Boey, S. K. (Septiembre de 1998). «Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration». Biophysical Journal 75 (3): 1584-1597. ISSN 0006-3495. PMC 1299832. PMID 9726959. doi:10.1016/S0006-3495(98)74076-7. Consultado el 29 de octubre de 2023. 
  17. ↑ Galbraith, C. G.; Sheetz, M. P. (19 de agosto de 1997). «A micromachined device provides a new bend on fibroblast traction forces». Proceedings of the National Academy of Sciences of the United States of America 94 (17): 9114-9118. ISSN 0027-8424. PMID 9256444. doi:10.1073/pnas.94.17.9114. Consultado el 29 de octubre de 2023. 
  18. ↑ Sun, Yu; Wan, Kai-Tak; Roberts, Kenneth P.; Bischof, John C.; Nelson, Bradley J. (Diciembre de 2003). «Mechanical property characterization of mouse zona pellucida». IEEE transactions on nanobioscience 2 (4): 279-286. ISSN 1536-1241. PMID 15376919. doi:10.1109/tnb.2003.820273. Consultado el 29 de octubre de 2023. 
  19. ↑ Yang, S.; Saif, T. (16 de marzo de 2005). «Micromachined force sensors for the study of cell mechanics». Rev. Sci. Instrum. 76 (4): 1-8. doi:10.1063/1.1863792. Consultado el 29 de octubre de 2023. 
  20. ↑ Park, Jungyul; Ryu, Jaewook; Choi, Seung Kyu; Seo, Eunseok; Cha, Jae Min; Ryu, Seokchang; Kim, Jinseok; Kim, Byungkyu et al. (15 de octubre de 2005). «Real-time measurement of the contractile forces of self-organized cardiomyocytes on hybrid biopolymer microcantilevers». Analytical Chemistry 77 (20): 6571-6580. ISSN 0003-2700. PMID 16223242. doi:10.1021/ac0507800. Consultado el 29 de octubre de 2023. 
  21. ↑ Aravamudhan, S. (2012). «A volume in Woodhead Publishing Series in Biomaterials.». Anal. Chem.: 81-96. 
  22. ↑ Louizos, Louizos-Alexandros; Athanasopoulos, Panagiotis G.; Varty, Kevin (Noviembre de 2012). «Microelectromechanical Systems and Nanotechnology: A Platform for the Next Stent Technological Era». Vascular and Endovascular Surgery (en inglés) 46 (8): 605-609. ISSN 1538-5744. doi:10.1177/1538574412462637. Consultado el 29 de octubre de 2023. 
  23. ↑ Thrivikraman, Greeshma; Boda, Sunil Kumar; Basu, Bikramjit (Enero de 2018). «Unraveling the mechanistic effects of electric field stimulation towards directing stem cell fate and function: A tissue engineering perspective». Biomaterials 150: 60-86. ISSN 1878-5905. PMID 29032331. doi:10.1016/j.biomaterials.2017.10.003. Consultado el 29 de octubre de 2023. 
  24. ↑ Titushkin, Igor; Cho, Michael (Enero de 2009). «Regulation of cell cytoskeleton and membrane mechanics by electric field: role of linker proteins». Biophysical Journal 96 (2): 717-728. ISSN 1542-0086. PMC 2716454. PMID 19167316. doi:10.1016/j.bpj.2008.09.035. Consultado el 29 de octubre de 2023. 
  25. ↑ Levin, Michael (1 de diciembre de 2014). «Molecular bioelectricity: how endogenous voltage potentials control cell behavior and instruct pattern regulation in vivo». Molecular Biology of the Cell 25 (24): 3835-3850. ISSN 1939-4586. PMC 4244194. PMID 25425556. doi:10.1091/mbc.E13-12-0708. Consultado el 29 de octubre de 2023. 
  26. ↑ Silver, Brian B.; Nelson, Celeste M. (2018). «The Bioelectric Code: Reprogramming Cancer and Aging From the Interface of Mechanical and Chemical Microenvironments». Frontiers in Cell and Developmental Biology 6: 21. ISSN 2296-634X. PMC 5845671. PMID 29560350. doi:10.3389/fcell.2018.00021. Consultado el 29 de octubre de 2023. 
  27. ↑ Yuan, Xiaoning; Arkonac, Derya E.; Chao, Pen-hsiu Grace; Vunjak-Novakovic, Gordana (14 de enero de 2014). «Electrical stimulation enhances cell migration and integrative repair in the meniscus». Scientific Reports 4: 3674. ISSN 2045-2322. PMC 3891019. PMID 24419206. doi:10.1038/srep03674. Consultado el 29 de octubre de 2023. 
  28. ↑ Rodriguez, M. L.; McGarry, P. J.; Sniadecki, N. J. (Noviembre de 2013). «Review on Cell Mechanics: Experimental and Modeling Approaches». Applied Mechanics Reviews 65 (6): 060801 (41 páginas). doi:10.1115/1.4025355. Consultado el 29 de octubre de 2023. 
  29. ↑ Arakawa, Mototaka; Shikama, Joe; Yoshida, Koki; Nagaoka, Ryo; Kobayashi, Kazuto; Saijo, Yoshifumi (Septiembre de 2015). «Development of an ultrasound microscope combined with optical microscope for multiparametric characterization of a single cell». IEEE transactions on ultrasonics, ferroelectrics, and frequency control 62 (9): 1615-1622. ISSN 1525-8955. PMID 26415124. doi:10.1109/TUFFC.2014.006865. Consultado el 29 de octubre de 2023. 
  30. ↑ a b Strohm, Eric; Czarnota, Gregory J.; Kolios, Michael C. (Octubre de 2010). «Quantitative measurements of apoptotic cell properties using acoustic microscopy». IEEE transactions on ultrasonics, ferroelectrics, and frequency control 57 (10): 2293-2304. ISSN 1525-8955. PMID 20889417. doi:10.1109/TUFFC.2010.1690. Consultado el 29 de octubre de 2023. 
  31. ↑ Daldrop, Peter; Brutzer, Hergen; Huhle, Alexander; Kauert, Dominik J.; Seidel, Ralf (19 de mayo de 2015). «Extending the range for force calibration in magnetic tweezers». Biophysical Journal 108 (10): 2550-2561. ISSN 1542-0086. PMC 4457047. PMID 25992733. doi:10.1016/j.bpj.2015.04.011. Consultado el 29 de octubre de 2023. 
  32. ↑ Neuman, Keir C.; Nagy, Attila (Junio de 2008). «Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy». Nature Methods 5 (6): 491-505. ISSN 1548-7105. PMC 3397402. PMID 18511917. doi:10.1038/nmeth.1218. Consultado el 29 de octubre de 2023. 
  33. ↑ Kim, Deok-Ho; Wong, Pak Kin; Park, Jungyul; Levchenko, Andre; Sun, Yu (2009). «Microengineered platforms for cell mechanobiology». Annual Review of Biomedical Engineering 11: 203-233. ISSN 1545-4274. PMID 19400708. doi:10.1146/annurev-bioeng-061008-124915. Consultado el 29 de octubre de 2023. 
  34. ↑ De Vlaminck, Iwijn; Dekker, Cees (2012). «Recent advances in magnetic tweezers». Annual Review of Biophysics 41: 453-472. ISSN 1936-1238. PMID 22443989. doi:10.1146/annurev-biophys-122311-100544. Consultado el 29 de octubre de 2023. 
  35. ↑ Monticelli, M.; Conca, D. V.; Albisetti, E.; Torti, A.; Sharma, P. P.; Kidiyoor, G.; Barozzi, S.; Parazzoli, D. et al. (19 de julio de 2016). «Magnetic domain wall tweezers: a new tool for mechanobiology studies on individual target cells». Lab on a Chip (en inglés) 16 (15): 2882-2890. ISSN 1473-0189. doi:10.1039/C6LC00368K. Consultado el 29 de octubre de 2023. 
  36. ↑ MacQueen, Luke; Sun, Yu; Simmons, Craig A. (6 de julio de 2013). «Mesenchymal stem cell mechanobiology and emerging experimental platforms». Journal of the Royal Society, Interface 10 (84): 20130179. ISSN 1742-5662. PMC 3673151. PMID 23635493. doi:10.1098/rsif.2013.0179. Consultado el 29 de octubre de 2023. 
  37. ↑ Puig-De-Morales, M.; Grabulosa, M.; Alcaraz, J.; Mullol, J.; Maksym, G. N.; Fredberg, J. J.; Navajas, D. (Septiembre de 2001). «Measurement of cell microrheology by magnetic twisting cytometry with frequency domain demodulation». Journal of Applied Physiology (Bethesda, Md.: 1985) 91 (3): 1152-1159. ISSN 8750-7587. PMID 11509510. doi:10.1152/jappl.2001.91.3.1152. Consultado el 29 de octubre de 2023. 
  38. ↑ Yang, Jen-Chang; Lee, Sheng-Yang; Chen, Chi-An; Lin, Che-Tong; Chen, Chang-Chih; Huang, Haw-Ming (Mayo de 2010). «The role of the calmodulin-dependent pathway in static magnetic field-induced mechanotransduction». Bioelectromagnetics 31 (4): 255-261. ISSN 1521-186X. PMID 19953573. doi:10.1002/bem.20559. Consultado el 29 de octubre de 2023. 
  39. ↑ Hughes, Jasmine Hannah; Kumar, Sanjay (Agosto de 2016). «Synthetic mechanobiology: engineering cellular force generation and signaling». Current Opinion in Biotechnology 40: 82-89. ISSN 1879-0429. PMC 4975654. PMID 27023733. doi:10.1016/j.copbio.2016.03.004. Consultado el 29 de octubre de 2023. 
  40. ↑ Wu, Congyu; Shen, Yajing; Chen, Mengwei; Wang, Kun; Li, Yongyong; Cheng, Yu (Abril de 2018). «Recent Advances in Magnetic-Nanomaterial-Based Mechanotransduction for Cell Fate Regulation». Advanced Materials (Deerfield Beach, Fla.) 30 (17): e1705673. ISSN 1521-4095. PMID 29543348. doi:10.1002/adma.201705673. Consultado el 29 de octubre de 2023. 
  41. ↑ Harshad, Kamble; Jun, Myeongjun; Park, Sungsu; Barton, Matthew J.; Vadivelu, Raja K.; St John, James; Nguyen, Nam-Trung (Junio de 2016). «An electromagnetic cell-stretching device for mechanotransduction studies of olfactory ensheathing cells». Biomedical Microdevices 18 (3): 45. ISSN 1572-8781. PMID 27194027. doi:10.1007/s10544-016-0071-1. Consultado el 29 de octubre de 2023. 
  42. ↑ K. H. Chiu et al., “Static magnetic fields promote osteoblast-like cells differentiation via increasing the membrane rigidity,” Ann. Biomed. Eng., vol. 35, no. 11, pp. 1932–1939, 2007
  43. ↑ Sbalzarini, Ivo F. (Mayo de 2013). «Modeling and simulation of biological systems from image data». BioEssays: News and Reviews in Molecular, Cellular and Developmental Biology 35 (5): 482-490. ISSN 1521-1878. PMC 3674526. PMID 23533152. doi:10.1002/bies.201200051. Consultado el 29 de octubre de 2023. 
  44. ↑ a b Escribano, J.; Sánchez, M. T.; García-Aznar, J. M. (1 de junio de 2014). «A discrete approach for modeling cell–matrix adhesions». Computational Particle Mechanics (en inglés) 1 (2): 117-130. ISSN 2196-4386. doi:10.1007/s40571-014-0006-7. Consultado el 29 de octubre de 2023. 
  45. ↑ a b Van Liedekerke, P.; Palm, M. M.; Jagiella, N.; Drasdo, D. (1 de diciembre de 2015). «Simulating tissue mechanics with agent-based models: concepts, perspectives and some novel results». Computational Particle Mechanics (en inglés) 2 (4): 401-444. ISSN 2196-4386. doi:10.1007/s40571-015-0082-3. Consultado el 29 de octubre de 2023. 
  46. ↑ Lowengrub, J. S.; Frieboes, H. B.; Jin, F.; Chuang, Y.-L.; Li, X.; Macklin, P.; Wise, S. M.; Cristini, V. (2010). «Nonlinear modelling of cancer: bridging the gap between cells and tumours». Nonlinearity 23 (1): R1-R9. ISSN 0951-7715. PMC 2929802. PMID 20808719. doi:10.1088/0951-7715/23/1/r01. Consultado el 29 de octubre de 2023. 
  47. ↑ Dallon, J. C.; Sherratt, J. A.; Maini, P. K. (21 de agosto de 1999). «Mathematical modelling of extracellular matrix dynamics using discrete cells: fiber orientation and tissue regeneration». Journal of Theoretical Biology 199 (4): 449-471. ISSN 0022-5193. PMID 10441462. doi:10.1006/jtbi.1999.0971. Consultado el 29 de octubre de 2023. 
Obtenido de «https://es.wikipedia.org/w/index.php?title=Mecanobiología&oldid=154938835»