Plano complejo
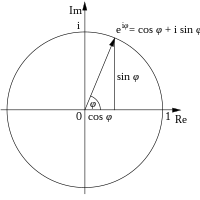
En matemáticas, el plano complejo es una forma de visualizar y ordenar el conjunto de los números complejos. Puede entenderse como un plano cartesiano modificado, en el que la parte real está representada en el eje de abscisas y la parte imaginaria en el eje de ordenadas. El eje de abscisas también recibe el nombre de eje real y el eje de ordenadas el nombre de eje imaginario. Asimismo, el conjunto de los números complejos se puede representar en su forma polar o trigonométrica, formando así un plano polar, en el que el valor absoluto, módulo o magnitud representa la longitud de un vector y su argumento es equivalente al ángulo del mencionado vector, excepto el complejo 0 que no tiene argumento.
Generalidades editar
El plano complejo a veces recibe el nombre de plano de Argand a causa de su uso en diagramas de Argand. Su creación se atribuye a Jean-Robert Argand, aunque fue inicialmente descrito por el encuestador y matemático Noruego-danés Caspar Wessel.
El concepto de plano complejo permite interpretar geométricamente los números complejos. La suma de números complejos se puede relacionar con la suma con vectores, y la multiplicación de números complejos puede expresarse simplemente usando coordenadas polares, donde la magnitud del producto es el producto de las magnitudes de los términos, y el ángulo contado desde el eje real del producto es la suma de los ángulos de los términos.
Los diagramas de Argand se usan frecuentemente para mostrar las posiciones de los polos y los ceros de una función en el plano complejo.
El análisis complejo, la teoría de las funciones analíticas, es una de las áreas más ricas de la matemática, que encuentra aplicación en muchas otras áreas de la matemática así como en física, electrónica y muchos otros campos.
Uso del plano complejo en teoría de control editar
En teoría de control, uno de los usos del plano complejo se conoce como el 'plano s'. Se usa para visualizar la ubicación de las raíces y de los ceros de la función de transferencia de un sistema LTI. La visualización gráfica de las raíces (es decir de aquellos valores que anulan la ecuación característica) y de los ceros (aquellos valores que anulan el numerador de la función de transferencia) permite inferir el comportamiento del sistema (por ejemplo permite saber si el sistema es estable o inestable). La función de transferencia se expresa normalmente como un cociente de polinomios de la variable 's' de la transformada de Laplace, y de ahí el nombre de plano 's'.
Además, otro uso del plano 's' es el criterio de estabilidad de Nyquist, que es un principio geométrico que permite determinar la estabilidad de un sistema de control mediante la inspección del diagrama de Nyquist de la respuesta de fase de la función de transferencia en el plano complejo.
El plano z es una versión de tiempo discreto del plano s, donde se utiliza la transformada Z en lugar de la de Laplace.
Véase también editar
Enlaces externos editar
- Wikimedia Commons alberga una categoría multimedia sobre Plano complejo.
- Weisstein, Eric W. «Argand Diagram». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.