Problema de Hansen
El Problema de Hansen es un caso de resolución geométrica que se presenta en topografía clásica plana. Recibe su nombre del astrónomo Peter Andreas Hansen (1795-1874), que trabajó en el estudio geodésico de Dinamarca.
Planteamiento
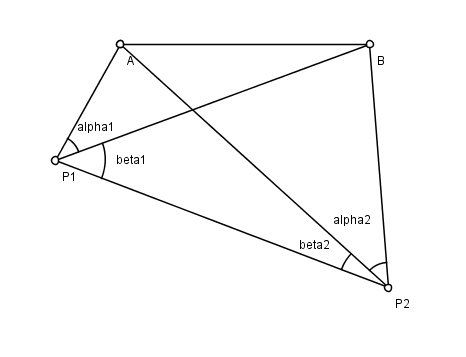
editarSe tienen dos puntos de coordenadas conocidas A y B, y otros dos puntos de coordenadas desconocidas P1 y P2. Desde P1 y P2 un observador mide el ángulo formado por las visuales a cada uno de los otros tres puntos. El problema es encontrar las posiciones de P1 y P2. De acuerdo con la figura, los ángulos medidos son (α1, β1, α2, y β2).
Puesto que implica la observación de ángulos desde puntos desconocidos, el problema es un ejemplo de resección (diferente de los problemas de intersección).
Ejemplo: este procedimiento permite valerse de dos referencias lejanas, cuya distancia entre sí se conoce (por ejemplo, los campanarios de dos iglesias, que serían los puntos A y B), para calcular las coordenadas de una pareja cualquiera de puntos observables entre sí P1 y P2 desde los que también se puedan observar las referencias lejanas.
Resumen del método de resolución
editarDefinir los siguientes ángulos: γ = P1AP2, δ = P1BP2, φ = P2AB, ψ = P1BA. Como primer paso, se resuelve para φ y ψ. La suma de estos dos ángulos desconocidos es igual a la suma de β1 y β2, resultando la ecuación
Una segunda ecuación puede encontrarse de forma algo más laboriosa como sigue. La ley de los senos establece que
- y
Combinando las dos expresiones, se obtiene
Con el mismo razonamiento en el otro lado, se tiene que
Relacionando ambas expresiones, se obtiene
Mediante una conocida identidad trigonométrica, este cociente de senos puede ser expresado como la tangente de una diferencia de ángulos:
De aquí se obtiene una segunda ecuación. Una vez que se resuelve el sistema de dos ecuaciones con dos incógnitas y , se puede utilizar cualquiera de las dos expresiones anteriores para con determinar P1 y P2 debido a que se conoce la distancia AB. Entonces es posible calcular todos los segmentos utilizando la ley de los senos.[1]
Algoritmo de la solución
editarDados los cuatro ángulos (α1, β1, α2, β2) y la distancia AB, el procedimiento de cálculo tiene el siguiente desarrollo:
- Calcular
- Calcular
- Hacer que y luego
- Calcular
- o de forma equivalente
- (Si una de estas dos fracciones tiene un denominador próximo a cero, utilizar la otra).
Véase también
editarReferencias
editar- ↑ Udo Hebisch: Ebene und Sphaerische Trigonometrie, Kapitel 1, Beispiel 4 (2005, 2006)[1] Archivado el 22 de febrero de 2016 en Wayback Machine.