Baricentro

En física, el baricentro de un cuerpo material coincide con el centro de masas del mismo cuando el cuerpo es homogéneo (densidad uniforme) o cuando la distribución de materia en el cuerpo tiene ciertas propiedades, tales como la simetría. Se distingue del centroide en geometría, donde el baricentro de una superficie contenida en una figura geométrica plana es un punto tal que cualquier recta que pasa por él divide a dicho segmento en dos partes de igual momento respecto a dicha recta.

Si uno de los dos cuerpos en órbita es mucho más masivo que el otro y los cuerpos están relativamente cerca uno del otro, el baricentro normalmente se ubicará dentro del objeto más masivo. En este caso, en lugar de que los dos cuerpos parezcan orbitar alrededor de un punto entre ellos, el cuerpo menos masivo parecerá orbitar alrededor del cuerpo más masivo, mientras que se puede observar que el cuerpo más masivo se tambalea ligeramente. Este es el caso del sistema Tierra-Luna, cuyo baricentro se encuentra en promedio a 4671 kilómetros (2902,4 mi) del centro de la Tierra, que es el 75% del radio de la Tierra de 6378 kilómetros (3963,1 mi).

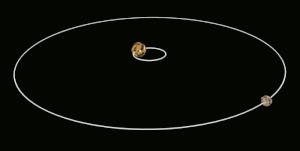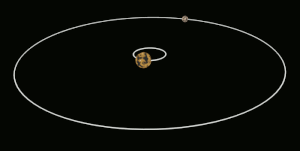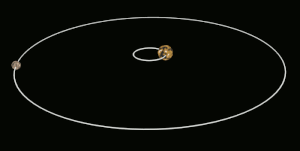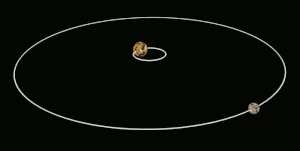
Cuando los dos cuerpos son de masas similares, el baricentro generalmente se ubicará en un punto entre ellos y ambos cuerpos orbitarán alrededor de él. Este es el caso de Plutón y Caronte, uno de los satélites naturales de Plutón, así como de muchos asteroides binarios y estrellas binarias. Cuando el objeto menos masivo está lejos, el baricentro puede ubicarse fuera del objeto más masivo. Este es el caso de Júpiter y el Sol; a pesar de que el Sol es mil veces más masivo que Júpiter, su baricentro está ligeramente fuera del Sol debido a la distancia relativamente grande entre ellos.^[1]

Problema de los dos cuerpos editar

Artículo principal: Problema de los dos cuerpos

El baricentro es uno de los focos de la órbita elíptica de cada cuerpo en cuestión. Este es un concepto importante en los campos de la astronomía y la astrofísica. Si a es el semieje mayor del sistema, r₁ es el semieje mayor de la órbita del primario alrededor del baricentro, y r₂ = a − r₁ es el semieje mayor de la órbita del secundario. Cuando el baricentro está ubicado dentro del cuerpo más masivo, ese cuerpo parecerá "tambalearse" en lugar de seguir una órbita perceptible. En un caso simple de dos cuerpos, la distancia del centro del primario al baricentro, r₁, viene dada por:

r_{1}=a\cdot {\frac {m_{2}}{m_{1}+m_{2}}}={\frac {a}{1+{\frac {m_{1}}{m_{2}}}}}

donde :

r₁ es la distancia del centro del cuerpo 1 al baricentro

a es la distancia entre los centros de los dos cuerpos

m₁ and m₂ son las masas de los dos cuerpos.

Cálculo del baricentro editar

Sean A₁, …, A_n n puntos, y m₁, …, m_n n números (m como masa). Entonces el baricentro de los (A_i, m_i) es el punto G definido como sigue:

{\overrightarrow {OG\,}}={\frac {\sum {m_{i}{\overrightarrow {O\!A_{i}}}}}{\sum {m_{i}}}}={\frac {m_{1}{\overrightarrow {O\!A_{1}}}+...+m_{n}{\overrightarrow {O\!A_{n}}}}{m_{1}+...+m_{n}}},\quad {\mbox{con}}\quad \sum {m_{i}}\neq 0\,.

Esta definición no depende del punto O, que puede ser cualquiera. Si se toma el origen del plano o del espacio se obtienen las coordenadas del baricentro como promedio ponderado por los m_i de las coordenadas de los puntos A_i:

x_{G}={\frac {\sum {m_{i}x_{i}}}{\sum {m_{i}}}}={\frac {m_{1}x_{1}+...+m_{n}x_{n}}{m_{1}+...+m_{n}}}\,.

La definición anterior equivale a la fórmula siguiente, más práctica para el cálculo vectorial, pues prescinde de las fracciones (se obtiene tomando O = G):

\sum _{i=1}^{n}{m_{i}{\overrightarrow {G\!A_{i}}}}={\vec {0}}\quad {\mbox{o bien}}\quad m_{1}{\overrightarrow {G\!A_{1}}}+...+m_{n}{\overrightarrow {G\!A_{n}}}={\vec {0}}\,.

Conceptos relacionados editar

Un isobaricentro (iso: mismo) es un baricentro con todas las masas iguales entre sí; es usual en tal caso tomarlas iguales a 1. Si no se precisan las masas, el baricentro es por defecto el isobaricentro.

El baricentro coincide con el concepto físico de centro de masa de un cuerpo material en tanto que el cuerpo sea homogéneo. La coincidencia del baricentro y el centro de masa permite localizar el primero de una forma sencilla. Si tomamos una superficie recortada en una cartulina y la sujetamos verticalmente desde cualquiera de sus puntos, girará hasta que el centro de gravedad (baricentro) se sitúe justamente en la vertical del punto de sujeción; marcando dicha vertical sobre la cartulina y repitiendo el proceso sujetando desde un segundo punto, encontraremos el baricentro en el punto de intersección.

Concepto físico editar

En Física, el centroide, el centro de gravedad y el centro de masa pueden, bajo ciertas circunstancias, coincidir entre sí, aunque designan conceptos diferentes. El centroide es un concepto puramente geométrico que depende de la forma del sistema; el centro de masas depende de la distribución de materia, mientras que el centro de gravedad depende del campo gravitatorio.

Consideremos un cuerpo material:

Para que el centroide del cuerpo coincida con el centro de masa, el cuerpo debe tener densidad uniforme o una distribución de materia que presente ciertas propiedades, tales como la simetría.
Para que un centro de masa del cuerpo coincida con el centro de gravedad, el cuerpo debe estar bajo la influencia de un campo gravitatorio uniforme.

Una figura cóncava puede tener su centroide en un punto situado fuera de la misma figura.

Propiedades algebraicas editar

Las propiedades algebraicas del baricentro son:

Homogeneidad: el baricentro no cambia si se multiplica todas las masas por un mismo factor k ≠ 0.

Formalmente: bar { (A₁, m₁), …, (A_n, m_n) } = bar { (A₁, km₁), …, (A_n, km_n) }.

Asociatividad: el baricentro se puede calcular reagrupando puntos, es decir introduciendo baricentros parciales.

Por ejemplo, si D = bar {(A, a), (B, b)} (con a + b ≠ 0) entonces bar {(A, a), (B, b), (C, c)} = bar {(D,a + b), (C, c)} (a + b + c ≠ 0)

Ejemplos editar

Ejemplo 1

Dado el centro de masa de un triángulo ABC. Sea I = bar { (B, 1), (C, 1)}, entonces G = bar {(A, 1), (B, 1), (C, 1)} = bar {(A, 1), (I, 2)}, lo que significa que G está en el segmento [A,I], a un tercio del camino a partir de I.

Ejemplo 2

Baricentro de una medialuna (véase ejemplo 2)

El baricentro se puede definir en las matemáticas con coeficientes negativos. Como no existen masas negativas, ¿qué significado físico se puede atribuir a estos cálculos? He aquí un ejemplo muy sencillo: en una hoja de cartón se ha recortado una "medialuna" como lo muestra la figura, constituida de un círculo amarillo, con centro B, en el cual hemos eliminado otro círculo de radio dos veces menor, con centro A. Se pregunta por el centro de masa de esa medialuna.

El cálculo resulta muy simplificado si consideramos a la "medialuna" como una yuxtaposición de dos discos, uno grande con masa positiva, y otro pequeño, con masa negativa. Las masas son proporcionales a las áreas (densidad uniforme), lo que daría una masa de 4 para el primer disco, y de -1 para el segundo. Entonces G = bar {(A, -1), (B, 4)}.

Cálculo geométrico del baricentro editar

El cálculo geométrico (con regla y compás) del baricentro de un polígono (regular o irregular), de n vértices, se puede realizar de la siguiente forma:

Se descompone el polígono en triángulos y cuadriláteros disjuntos (que no tengan vértices en común). Se calculan los baricentros de estos triángulos y cuadriláteros, y se forma el polígono correspondiente.

Se puede probar que este algoritmo tiene orden logarítmico.

Véase también editar

Referencias editar

↑ MacDougal, Douglas W. (December 2012). Newton's Gravity: An Introductory Guide to the Mechanics of the Universe. Berlin: Springer Science & Business Media. p. 199. ISBN 978-1-4614-5444-1.

Datos: Q809690
Multimedia: Barycenter / Q809690

[MacDougal-1] MacDougal, Douglas W. (December 2012). Newton's Gravity: An Introductory Guide to the Mechanics of the Universe. Berlin: Springer Science & Business Media. p. 199. ISBN 978-1-4614-5444-1.

[1]