Grafo complemento

En teoría de grafos, el grafo complemento o complementario de un grafo es otro grafo, con el mismo conjunto de vértices del original, y tal que dos vértices están conectados por una arista si y solo si esa arista no existe en el primero.​ Para obtener el complemento de un grafo, se pueden completar todas las aristas faltantes para hacerlo completo, y quitar todas las aristas del grafo G original. Note que esta definición aplica tanto para grafos dirigidos como no dirigidos.​ Este concepto no debe confundirse con el del complemento de un conjunto, pues solo se complementan las aristas.

El grafo de Petersen (a la izquierda) y su grafo complemento (a la derecha).

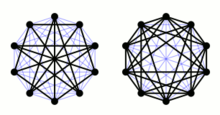
Por definición, los conjuntos de aristas de un grafo y su grafo complemento forman una partición; es decir, su intersección es vacía y su unión es el conjunto de todas las aristas posibles que tendría el grafo completo del mismo número de vértices.​

Se llama grafo autocomplementario a aquel que es isomorfo a su propio complemento.

Este tipo de grafos no debe confundirse con el grafo inverso. Si dos vértices de un grafo no están conectados por aristas, el grafo inverso conservará dicha ausencia de aristas, mientras que el grafo complemento los conectará con aristas en ambos sentidos. Asimismo, si dos vértices de un grafo dirigido están conectados en ambos sentidos, el grafo inverso conservará dichas aristas, mientras que el grafo complemento eliminará las aristas entre ambos vértices.​

Definición formal

Dado un grafo $G=(V,E)$, con $V$ su conjunto de vértices, $n=|V|$, y $E$ su conjunto de aristas o arcos, el grafo complemento de $G$ es el grafo $G'=(V',E')$ definido por:

• $V'=V$, y
• $E'=E_{K}\setminus E$, donde $E_{K}$ es el conjunto de aristas del grafo completo $K_{n}=(V,E_{K})$.

Aplicaciones

El grafo complemento se utiliza en muchos ámbitos de la teoría de grafos y en demostraciones, tales como la Teoría de Ramsey o diferentes reducciones para pruebas de NP-Completitud.

Véase también

• Grafo inverso

Bibliografía

• Wasserman, Stanley; Faust, Katherine (2013) [1994]. Análisis de redes sociales: Métodos y aplicaciones. Madrid: Centro de Investigaciones Sociológicas. ISBN 978-84-7476-631-8. OCLC 871814053. 

• Datos: Q902252
• Multimedia: Complement graph / Q902252