Prueba de la línea horizontal
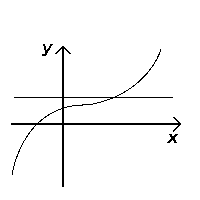 Pasa la prueba (inyectiva) |
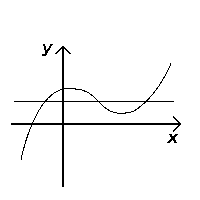 Falla la prueba (no inyectiva) |
En matemáticas, la prueba de la línea horizontal es una comprobación utilizada para determinar si una función es inyectiva (es decir, si presenta una correspondencia uno a uno entre los valores de su dominio y de su imagen).[1]
En el cálculo
editarUna línea horizontal es una línea recta y sin pendiente que discurre de izquierda a derecha. Dada una función (es decir, una aplicación de los números reales en los números reales), se puede determinar si es una función inyectiva observando las líneas horizontales que se cruzan con la gráfica de la función. Si alguna línea horizontal corta el gráfico en más de un punto, la función no es inyectiva. Para ver esto, basta tener en cuenta que los puntos de intersección tienen el mismo valor (porque se encuentran en la línea ) pero diferentes valores de , lo que por definición significa que la función no puede ser inyectiva.[1]
Se pueden usar variantes de la prueba de la línea horizontal para determinar si una función es sobreyectiva o biyectiva:
- La función f es sobreyectiva (es decir, se aplica en) bicondicionalmente si su gráfico interseca cualquier línea horizontal al menos una vez.
- La función f es biyectiva si y solo si cualquier línea horizontal se cruza con el gráfico exactamente una vez.
En la teoría de conjuntos
editarConsidérese una función con su gráfica correspondiente como un subconjunto del producto cartesiano . Sean las líneas horizontales en : . La función f es inyectiva bicondicionalmente, si cada línea horizontal interseca el gráfico como máximo una vez. En este caso, se dice que el gráfico pasa la prueba de la línea horizontal. Si alguna línea horizontal interseca el gráfico más de una vez, la función falla la prueba de la línea horizontal y no es inyectiva.[2]
Véase también
editarReferencias
editar- ↑ a b Stewart, James (2003). Single Variable Calculus: Early Transcendentals (5th. edición). Toronto ON: Brook/Cole. pp. 64. ISBN 0-534-39330-6. Consultado el 15 de julio de 2012. «Por lo tanto, disponemos del siguiente método geométrico para determinar si una función presenta una correspondencia uno-a-uno.»
- ↑ Zorn, Arnold Ostebee, Paul (2002). Calculus from graphical, numerical, and symbolic points of view (2nd edición). Australia: Brooks/Cole/Thomson Learning. p. 185. ISBN 0-03-025681-X. «Ninguna línea horizontal cruza el gráfico f más de una vez.»