Altura (triángulo)

En geometría plana, una altura de un triángulo es cada uno de los segmentos que une un vértice con un punto de su lado opuesto o de su prolongación y es perpendicular a dicho lado.

Las tres alturas de un triángulo se cruzan en el ortocentro, que para un triángulo agudo se encuentra dentro del triángulo.

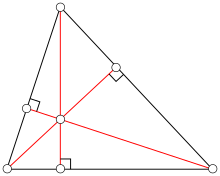
Términos y caracterizaciones

El extremo de la altura que está en la base o su prolongación, se denomina pie de la altura. La longitud de la altura, a menudo simplemente llamada "la altura", es la distancia entre la base (extendida en su caso si se trata de un triángulo obtuso) y el vértice. El proceso de dibujar la altura desde el vértice al pie se conoce como "bajar la altura" desde ese vértice. Es un caso especial de proyección.

Las alturas se pueden usar en el cálculo del área de un triángulo: el semiproducto de la longitud de una altura y la longitud de su base. Por lo tanto, la altura más larga es perpendicular al lado más corto del triángulo, pues cada altura es inversamente proporcional a su respectivo lado. Las alturas también están relacionadas con los lados del triángulo a través de fórmulas trigonométricas.

En un triángulo rectángulo, las alturas de cada ángulo agudo coinciden con un cateto del triángulo, e intersecan el lado opuesto (tienen su pie) en el vértice del ángulo recto, que es el ortocentro.

En un triángulo isósceles (un triángulo con dos lados congruentes), la altura que tiene el lado incongruente como base tendrá el punto medio de ese lado como su pie. También la altura que tiene el lado incongruente como su base será la bisectriz del ángulo del vértice.

Es común marcar la altura con la letra h, a menudo acompañada con la letra del lado sobre el que se levanta.

En un triángulo rectángulo, la altura trazada sobre la hipotenusa c, divide la hipotenusa en dos segmentos de longitudes p y q. Si se denomina la longitud de la altura por h_c, entonces se verifica la relación

$h_{c}={\sqrt {pq}}$ (Teorema geométrico principal)

Las alturas de cada uno de los ángulos agudos de un triángulo obtuso se encuentran completamente fuera del triángulo, al igual que el ortocentro H.

Para triángulos agudos y rectángulos, los pies de las alturas caen todos sobre los lados del triángulo (no extendidos). En un triángulo obtuso, el pie de la altura desde el vértice del ángulo obtuso cae en el interior del lado opuesto, pero los pies de las alturas a los vértices de los ángulos agudos caen en el lado extendido, en el exterior al triángulo Esto se ilustra en el diagrama adyacente: en este triángulo obtuso, una altura trazada perpendicularmente desde el vértice superior, que tiene un ángulo agudo, corta el lado horizontal extendido fuera del triángulo.

Ortocentro

Véase también: Sistema ortocéntrico

Las tres alturas (extendidas en algunos casos) se cortan en un solo punto, llamado ortocentro del triángulo, generalmente denotado por H.​​ El ortocentro se encuentra dentro del triángulo si y solo si el triángulo es agudo (es decir, no tiene ángulo mayor o igual a un ángulo recto). Si uno de los ángulos es recto, el ortocentro coincide con el vértice de este ángulo.​

Sean A, B, C los vértices y también los ángulos de un triángulo, y sean a = |BC|, b = |CA|, c = |AB| las longitudes de los lados. El ortocentro tiene coordenadas trilineales​

$\sec A:\sec B:\sec C=\cos A-\operatorname {sen} B\operatorname {sen} C:\cos B-\operatorname {sen} C\operatorname {sen} A:\cos C-\operatorname {sen} A\operatorname {sen} B,$

y coordenadas baricéntricas

$\displaystyle (a^{2}+b^{2}-c^{2})(a^{2}-b^{2}+c^{2}):(a^{2}+b^{2}-c^{2})(-a^{2}+b^{2}+c^{2}):(a^{2}-b^{2}+c^{2})(-a^{2}+b^{2}+c^{2})$

$=\tan A:\tan B:\tan C.$

Como las coordenadas baricéntricas son todas positivas para un punto en el interior de un triángulo, pero al menos una es negativa para un punto en el exterior, y dos de las coordenadas baricéntricas son cero para un punto de vértice, las coordenadas baricéntricas dadas para el ortocentro muestran que el ortocentro está en el interior de un triángulo agudo, en el vértice del ángulo recto de un triángulo rectángulo y en el exterior a un triángulo obtuso.

Dado el plano complejo, sean los puntos A, B y C, que representan respectivamente los números complejos $z_{A}$, $z_{B}$ y $z_{C}$ y supóngase que el circuncentro del triángulo ABC se encuentra en el origen del plano. Entonces, el número complejo

$z_{H}=z_{A}+z_{B}+z_{C}$

está representado por el punto H, es decir, el ortocentro del triángulo ABC.​ A partir de esto, las siguientes caracterizaciones del ortocentro H mediante vectores libres se pueden establecer de manera directa:

${\vec {OH}}=\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {OA}},\qquad 2\cdot {\vec {HO}}=\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {HA}}.$

La primera de las identidades vectoriales previas también se conoce como el "problema de Sylvester", propuesto por James Joseph Sylvester.​

Propiedades

Sean D, E y F los pies de las alturas de A, B y C, respectivamente. Entonces:

• El producto de las longitudes de los segmentos en los que el ortocentro divide una altura es el mismo para las tres alturas:​​

$AH\cdot HD=BH\cdot HE=CH\cdot HF.$

El círculo centrado en H que tiene por radio la raíz cuadrada de esta constante es el círculo polar.​ del triángulo

• La suma de los cocientes (para las tres alturas) resultantes de dividir la distancia del ortocentro desde la base por la longitud de la altura es 1:​ (Esta propiedad y la siguiente son aplicaciones de una propiedad más general de cualquier punto interior y de las tres cevianas que lo atraviesan)

${\frac {HD}{AD}}+{\frac {HE}{BE}}+{\frac {HF}{CF}}=1.$

• La suma de las relaciones en las tres alturas de la distancia del ortocentro desde el vértice a la longitud de la altura es 2:​

${\frac {AH}{AD}}+{\frac {BH}{BE}}+{\frac {CH}{CF}}=2.$

• El conjugado isogonal del ortocentro es el circuncentro del triángulo.​

• El conjugado isotómico del ortocentro es el punto simediano del triángulo anticomplementario.​

• Cuatro puntos en el plano, de modo que uno de ellos es el ortocentro del triángulo formado por los otros tres, se denominan un sistema ortocéntrico o cuadrilátero ortocéntrico.

Relación con círculos y cónicas

Sea R el circunradio de un triángulo. Entonces​​

$a^{2}+b^{2}+c^{2}+AH^{2}+BH^{2}+CH^{2}=12R^{2}.$

Además, siendo r el radio de la circunferencia inscrita, y siendo r_a, r_b y r_c los radios de sus circunferencias exinscritas, y R de nuevo como el radio de su circunferencia circunscrita, las siguientes relaciones se mantienen con respecto a las distancias del ortocentro desde los vértices:​

$r_{a}+r_{b}+r_{c}+r=AH+BH+CH+2R,$

$r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}=AH^{2}+BH^{2}+CH^{2}+(2R)^{2}.$

Si cualquier altura, por ejemplo, AD, se extiende para intersecar la circunferencia circunscrita en P, de modo que AP es una cuerda de la circunferencia, entonces el pie D divide el segmento HP:​

$HD=DP.$

Las directrices de todas las parábolas que son tangentes externamente a un lado de un triángulo y tangentes a las extensiones de los otros lados pasan por el ortocentro.​

Una circuncónica que pasa por el ortocentro de un triángulo es una hipérbola.​

Relación con otros centros, el círculo de nueve puntos

El ortocentro H, el centroide G, el circuncentro O y el centro N de la circunferencia de los nueve puntos se encuentran en una sola línea, conocida como recta de Euler.​ El centro de la circunferencia de nueve puntos se encuentra en el punto medio de la línea de Euler, entre el ortocentro y el circuncentro, y la distancia entre el centroide y el circuncentro es la mitad de la existente entre el centroide y el ortocentro:​

$OH=2NH,$

$2OG=GH.$

El ortocentro está más cerca del incentro I que del centroide, y el ortocentro está más alejado que el incentro del centroide:

$HI<HG,$

$HG>IG.$

En términos de los lados a, b, c, el radio de la circunferencia inscrita r y el radio de la circunferencia circunscrita R,​

$OH^{2}=R^{2}-8R^{2}\cos A\cos B\cos C=9R^{2}-(a^{2}+b^{2}+c^{2}),$​

$HI^{2}=2r^{2}-4R^{2}\cos A\cos B\cos C.$

Triángulo órtico

Triángulo abc (respectivamente, DEF en el texto) es el triángulo órtico del triángulo ABC

Si el triángulo ABC es oblicuo (no contiene un ángulo recto), el triángulo podal de las alturas del triángulo original se llama triángulo órtico o triángulo de alturas. Es decir, los pies de las alturas de un triángulo oblicuo forman el triángulo órtico DEF. Además, el incentro (el centro del círculo inscrito) del triángulo órtico DEF, coincide con el ortocentro del triángulo original ABC.​

Las coordenadas trilineales para los vértices del triángulo órtico vienen dadas por

• D = 0 : sec B : sec C
• E = sec A : 0 : sec C
• F = sec A : sec B : 0.

Los lados extendidos del triángulo órtico se encuentran con los lados extendidos opuestos de su triángulo de referencia en tres puntos alineados.​​​

En cualquier triángulo agudo, el triángulo inscrito con el perímetro más pequeño es el triángulo órtico.​ Esta es la solución al problema de Fagnano, planteado en 1775.​ Los lados del triángulo órtico son paralelos a las tangentes a la circunferencia circunscrita en los vértices del triángulo original.​

El triángulo órtico de un triángulo agudo da una ruta de luz triangular (un conjunto cíclico de tres reflexiones).​

Las líneas tangentes de la circunferencia de nueve puntos en los puntos medios de los lados de ABC son paralelos a los lados del triángulo órtico, formando un triángulo similar al triángulo órtico.​

El triángulo órtico está estrechamente relacionado con el triángulo tangencial, construido de la siguiente manera: sea L_A la línea tangente de la circunferencia circunscrita del triángulo ABC en el vértice A, y análogamente L_B y L_C. Sean también A" = L_B ∩ L_C, B" = L_C ∩ L_A, C" = L_C ∩ L_A. El triángulo tangencial es A"B"C", cuyos lados son las tangentes a la circunferencia circunscrita al triángulo ABC en sus vértices; es homotético al triángulo órtico. El circuncentro del triángulo tangencial y el centro de semejanza de los triángulos órtico y tangencial están en la recta de Euler.​

Las coordenadas trilineales para los vértices del triángulo tangencial están dadas por

• A" = −a : b : c
• B" = a : −b : c
• C" = a : b : −c.

Para obtener más información sobre el triángulo órtico, véase sistema ortocéntrico.

Algunos teoremas y resultados adicionales

Altura en función de los lados

Datos de trabajo

Sea el triángulo BAC, con la base BC = a, en posición horizontal, la altura h relativa del lado a, uno de ángulos debe ser agudo, para el caso C < 90°; H, pie de la altura AH = h. en el lado BC y HC = m, proyección ortogonal del lado b sobre el lado a.

Ejecución de los pasos

De los triángulos AHC y ABC resulta que se cumple:

(1) $h^{2}=b^{2}-b^{2}$ según el teorema de Pitágoras

(2)$c^{2}=a^{2}+b^{2}-2a\cdot m$ por teorema del cuadrado del lado opuesto de un ángulo agudo

Despejando m de (2), se reemplaza en (1),

teniendo h² se desarrolla algebraicamente, usando diferencia de cuadrados; finalmente, cuando se tiene en el numerador cuatro factores lineales

$h^{2}={\frac {p(p-a)(p-b)(p-c)}{4a^{2}}}$, siendo $p={\frac {a+b+c}{2}}$ el semiperímetro

se halla la

Fórmula de la altura

$h={\frac {2}{a}}\times {\sqrt {p(p-a)(p-b)(p-c)}}$​

Área según Herón

Empleando la fórmula anterior se aplica al cálculo de área triangular: $A_{\Delta }={\frac {ah}{2}}$ resulta el área del triángulo $A_{\Delta }={\sqrt {p(p-a)(p-b)(p-c)}}$

Las tres alturas

Se presentan las alturas de los tres lados de un triángulo

1. altura del lado a: $\ h_{a}={\frac {2}{a}}\times {\sqrt {p(p-a)(p-b)(p-c)}}$
2. altura del lado b: $\ h_{b}={\frac {2}{b}}\times {\sqrt {p(p-a)(p-b)(p-c)}}$
3. altura del lado c: $\ h_{c}={\frac {2}{c}}\times {\sqrt {p(p-a)(p-b)(p-c)}}$ ​

Si se hace $\ \alpha =2{\sqrt {p(p-a)(p-b)(p-c)}}$, las igualdades inmediatas anteriores dan $h_{a}={\frac {\alpha }{a}};\ h_{b}={\frac {\alpha }{b}};\ h_{c}={\frac {\alpha }{c}}$, lo que indica que las alturas son inversamente proporcionales a sus respectivos lados.

Teorema del inradio

Considérese un triángulo arbitrario con lados a, b, c y con las correspondientes alturas h_a, h_b y h_c. Las alturas y el radio de la circunferencia inscrita r están relacionados por​

$\displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}.$

Teorema del circunradio

Denominando la altura desde un lado de un triángulo como h_a, los otros dos lados como b y c, y el radio de la circunferencia circunscrita del triángulo como R, la altura viene dada por​

$h_{a}={\frac {bc}{2R}}.$

Punto interior

Si p₁, p₂ y p₃ son las distancias perpendiculares desde cualquier punto P a los lados, y h₁, h₂ y h₃ son las alturas a los lados respectivos, entonces​

${\frac {p_{1}}{h_{1}}}+{\frac {p_{2}}{h_{2}}}+{\frac {p_{3}}{h_{3}}}=1.$

Punto general en una altura

Si E es cualquier punto en una altura AD de un triángulo ABC, entonces​

$AC^{2}+EB^{2}=AB^{2}+CE^{2}.$

Casos especiales de triángulos

Triángulo equilátero

Para cualquier punto P dentro de un triángulo equilátero, la suma de las perpendiculares a los tres lados es igual a la altura del triángulo. Esta propiedad es conocida como el teorema de Viviani.

Triángulo rectángulo

En un triángulo rectángulo, las tres alturas h_a, h_b y h_c (las dos primeras son iguales a las longitudes de los catetos b y a, respectivamente) están relacionadas según​​

${\frac {1}{h_{a}^{2}}}+{\frac {1}{h_{b}^{2}}}={\frac {1}{h_{c}^{2}}}.$

Véase también

• Elementos notables de un triángulo
• Mediana (geometría)

Bibliografía

• Altshiller-Court, Nathan (2007) [1952], College Geometry, Dover Publications .
• Berele, Allan; Goldman, Jerry (2001), Geometry / Theorems and Constructions, Prentice Hall, ISBN 0-13-087121-4 .
• Johnson, Roger A. (2007) [1960], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0 .
• Smart, James R. (1998), Modern Geometries (5th edición), Brooks/Cole, ISBN 0-534-35188-3 .

Enlaces externos

• Weisstein, Eric W. «alturae». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Orthocenter of a triangle Con animación interactiva
• Demostración animada de la construcción del ortocentro Brújula y regla.
• Fagnano's Problem por Jay Warendorff, Wolfram Demonstrations Project.

• Datos: Q339495
• Multimedia: Height (triangle) / Q339495