Toroide
En geometría el toroide es la superficie de revolución generada por un polígono o una curva plana cerrada simple que gira alrededor de una recta exterior coplanar (el eje de rotación) con la que no se interseca.[1] Su forma se corresponde con la superficie de los objetos que, en el habla cotidiana, se denominan: argollas, anillos, aros, rosquilla, picarón o donut. La palabra toroide también se usa para referirse a un poliedro toroidal, la superficie de revolución generada por un polígono que gira alrededor de un eje.[2]

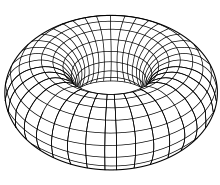

Cuando la curva cerrada es una circunferencia, la superficie se denomina «toro». En lenguaje cotidiano se llama «anillo» al cuerpo cuya superficie exterior es un «toro», lo que ilustra la diferencia entre una superficie y el volumen encerrado por ella.
Volumen
editarEl volumen encerrado por un toroide es:
donde R es la distancia del eje de rotación al isobaricentro de la figura plana generatriz y A el área limitada por dicha figura.
Diversas ecuaciones del toroide
editarEn un sistema de coordenadas cartesianas de centro O, ejes horizontales x e y y eje vertical z, la superficie del toro se puede generar del modo siguiente. Se construye sobre el plano xz una circunferencia de radio r con centro en el punto C que está sobre el eje x y a distancia R de O. La superficie del toro se genera cuando se hace girar esta circunferencia alrededor del eje z.
Ecuaciones paramétricas
editarLas coordenadas de un punto cualquiera del toro se obtienen mediante las siguientes expresiones, donde intervienen los parámetros: α es la latitud del punto respecto del plano xz, y β el ángulo de rotación de la circunferencia generatriz alrededor del eje z o longitud. Se tiene entonces que
A cualquier par ordenado de valores de los ángulos α y β le corresponde un punto del toro de coordenadas: x, y, z.
Ecuación cartesiana
editarPartiendo de las ecuaciones:
se puede eliminar el ángulo β. A partir de las siguientes ecuaciones, se puede también eliminar α:
Ecuación cartesiana
editarLa ecuación en coordenadas cartesianas de un toro cuyo eje de giro es el eje z, R la distancia del centro del círculo al eje y r el radio del círculo, es:
racionalizando
- [3]
donde la expresión de la derecha es la ecuación que deben satisfacer las coordenadas x, y, z de cualquier punto del toro.
Véase también
editarReferencias
editar- ↑ Real Academia Española. «toroide». Diccionario de la lengua española (23.ª edición).
- ↑ Weisstein, Eric W. «Toroide». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Santaló y otros: Geometría analítica