Sucesión de Fibonacci

En matemáticas, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales:

Gráfica de la sucesión de Fibonacci hasta $f_{10}$

$0,1,1,2,3,5,8,13,21,34,55\ldots \,$

El primer elemento es $0$, el segundo es $1$ y cada elemento restante es la suma de los dos anteriores. A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos.

Historia

La sucesión de Fibonacci en términos de conejos

Antes de que Fibonacci escribiera su trabajo, la sucesión de los números de Fibonacci había sido descubierta por matemáticos indios tales como Gopala (antes de 1135) y Hemachandra (c. 1150), quienes habían investigado los patrones rítmicos que se formaban con sílabas o notas de uno o dos pulsos. El número de tales ritmos (teniendo juntos una cantidad n de pulsos) era $f_{n+1}$, que produce explícitamente los números 1, 2, 3, 5, 8, 13, 21, etc.​

La sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos: "Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también".​

De esta manera Fibonacci presentó la sucesión en su libro Liber Abaci, publicado en 1202. Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, responsable de haberla denominado como se la conoce en la actualidad.​

También Kepler describió los números de Fibonacci, y el matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números de Fibonacci sucesivos $f_{n+1}/f_{n}$ se acerca a la relación áurea fi ($\varphi$) cuanto más se acerque $n$ a infinito; es más: el cociente de dos términos sucesivos de toda sucesión recurrente de orden dos tiende al mismo límite. Esta serie ha tenido popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók u Olivier Messiaen la han utilizado para la creación de acordes y de nuevas estructuras de frases musicales.

Definición formal

Los números de Fibonacci $f_{0},f_{1},f_{2},f_{3},\dots$ quedan definidos por las ecuaciones

(1)$f_{0}=0\,$

(2)$f_{1}=1\,$

(3)$f_{n}=f_{n-1}+f_{n-2}\,$ para $n=2,3,4,5,\ldots$

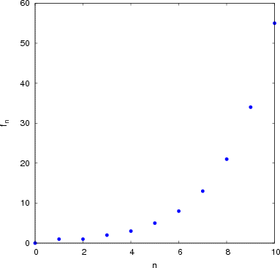
Esto produce los números

• $f_{0}=0\,$
• $f_{1}=1\,$
• $f_{2}=1\,$
• $f_{3}=2\,$
• $f_{4}=3\,$
• $f_{5}=5\,$
• $f_{6}=8\,$
• $f_{7}=13\,$
• $f_{8}=21\,$

y así sucesivamente hasta el infinito.

Representaciones alternativas

Para analizar la sucesión de Fibonacci (y, en general, cualquier sucesión) es conveniente obtener otras maneras de representarla matemáticamente.

Función generadora

Una función generadora para una sucesión cualquiera $a_{0},a_{1},a_{2},\dots$ es la función $f(x)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+\cdots$, es decir, una serie de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora

(4)$f\left(x\right)={\frac {x}{1-x-x^{2}}}$

Cuando esta función se expande en potencias de $x\,$, los coeficientes resultan ser la sucesión de Fibonacci:

${\frac {x}{1-x-x^{2}}}=0x^{0}+1x^{1}+1x^{2}+2x^{3}+3x^{4}+5x^{5}+8x^{6}+13x^{7}+\cdots$

Fórmula explícita

La definición de la sucesión de Fibonacci es recurrente; es decir que se necesitan calcular varios términos anteriores para poder calcular un término específico. Se puede obtener una fórmula explícita de la sucesión de Fibonacci (que no requiere calcular términos anteriores) notando que las ecuaciones (1), (2) y (3) definen la relación de recurrencia

$f_{n+2}-f_{n+1}-f_{n}=0\,$

con las condiciones iniciales

$f_{0}=0\,$ y $f_{1}=1\,$

El polinomio característico de esta relación de recurrencia es $t^{2}-t-1=0$, y sus raíces son

$t={\frac {1\pm {\sqrt {5}}}{2}}$

De esta manera, la fórmula explícita de la sucesión de Fibonacci tiene la forma

$f_{n}=b\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}+d\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}$

Si se toman en cuenta las condiciones iniciales, entonces las constantes $b$ y $d$ satisfacen la ecuación anterior cuando $n=0$ y $n=1$, es decir que satisfacen el sistema de ecuaciones

$\left.{\begin{array}{rcl}b+d&=&0\\b\left({\frac {1+{\sqrt {5}}}{2}}\right)+d\left({\frac {1-{\sqrt {5}}}{2}}\right)&=&1\end{array}}\right\}$

Al resolver este sistema de ecuaciones se obtiene

$b={\frac {1}{\sqrt {5}}},d=-{\frac {1}{\sqrt {5}}}$

Por lo tanto, cada número de la sucesión de Fibonacci puede ser expresado como

(5)$f_{n}={\frac {1}{\sqrt {5}}}\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-{\frac {1}{\sqrt {5}}}\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}$

Para simplificar aún más es necesario considerar el número áureo

$\varphi ={\frac {1+{\sqrt {5}}}{2}}$

de manera que la ecuación (5) se reduce a

(6)$f_{n}={\frac {\varphi ^{n}-\left(-\varphi \right)^{-n}}{\sqrt {5}}}$

Esta fórmula se le atribuye a Édouard Lucas, y es fácilmente demostrable por inducción matemática. A pesar de que la sucesión de Fibonacci consta únicamente de números naturales, su fórmula explícita incluye al número irracional $\varphi \,$. De hecho, la relación con este número es estrecha.

Forma matricial

Otra manera de obtener la sucesión de Fibonacci es considerando el sistema lineal de ecuaciones

$\left.{\begin{array}{rcl}f_{n}&=&f_{n}\\f_{n-1}+f_{n}&=&f_{n+1}\end{array}}\right\}$

Este sistema se puede representar mediante su notación matricial como

${\begin{bmatrix}0&1\\1&1\end{bmatrix}}{\begin{bmatrix}f_{n-1}\\f_{n}\end{bmatrix}}={\begin{bmatrix}f_{n}\\f_{n+1}\end{bmatrix}}$

Conociendo a $f_{0}=0$ y $f_{1}=1$, al aplicar la fórmula anterior $n$ veces se obtiene

(7)${\begin{bmatrix}0&1\\1&1\end{bmatrix}}^{n}{\begin{bmatrix}0\\1\end{bmatrix}}={\begin{bmatrix}f_{n}\\f_{n+1}\end{bmatrix}}$

y más aún

(8)${\begin{bmatrix}0&1\\1&1\end{bmatrix}}^{n}={\begin{bmatrix}f_{n-1}&f_{n}\\f_{n}&f_{n+1}\end{bmatrix}}$

Estas igualdades pueden probarse mediante inducción matemática.

Propiedades de la sucesión

Al construir bloques cuya longitud de lado sean números de Fibonacci se obtiene un dibujo que asemeja al rectángulo áureo (véase Número áureo).

Los números de Fibonacci aparecen en numerosas aplicaciones de diferentes áreas. Por ejemplo, en modelos de la crianza de conejos o de plantas, al contar el número de cadenas de bits de longitud $n$ que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes. De hecho, existe una publicación especializada llamada Fibonacci Quarterly​ dedicada al estudio de la sucesión de Fibonacci y temas afines. Se trata de un tributo a cuán ampliamente los números de Fibonacci aparecen en matemáticas y sus aplicaciones en otras áreas. Algunas de las propiedades de esta sucesión son las siguientes:

• La razón o cociente entre un término y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo. Es decir:

$\lim _{n\to \infty }{\frac {f_{n+1}}{f_{n}}}=\varphi$

Este límite no es privativo de la Sucesión de Fibonacci. Cualquier sucesión recurrente de orden 2, como la sucesión 3, 4, 7, 11, 18,..., lleva al mismo límite. Esto fue demostrado por Barr y Schooling en una carta publicada en la revista londinense "The Field" del 14 de diciembre de 1912. Los cocientes son oscilantes; es decir, que un cociente es menor al límite y el siguiente es mayor. Los cocientes pueden ordenarse en dos sucesiones que se aproximan asintóticamente por exceso y por defecto al valor límite.

• Cualquier número natural se puede escribir mediante la suma de un número limitado de términos de la sucesión de Fibonacci, cada uno de ellos distinto a los demás. Por ejemplo, $17=13+3+1$, $65=55+8+2$.
• Tan sólo un término de cada tres es par, uno de cada cuatro es múltiplo de 3, uno de cada cinco es múltiplo de 5, etc. Esto se puede generalizar, de forma que la sucesión de Fibonacci es periódica en las congruencias módulo $m$, para cualquier $m$.
• La sucesión puede expresarse mediante otra fórmula explícita llamada forma de Binet (de Jacques Binet). Si $\textstyle \alpha ={\frac {1+{\sqrt {5}}}{2}}$ y $\textstyle \beta ={\frac {1-{\sqrt {5}}}{2}}$, entonces

$f_{n}={\frac {\alpha ^{n}-\beta ^{n}}{\alpha -\beta }}$ y $f_{n}\approx {\frac {\alpha ^{n}}{\sqrt {5}}}\,$

• Cada número de Fibonacci es el promedio del término que se encuentra dos posiciones antes y el término que se encuentra una posición después. Es decir

$f_{n}={\frac {f_{n-2}+f_{n+1}}{2}}$

• La suma de los $n$ primeros números es igual al número que ocupa la posición $n+2$ menos uno. Es decir

$f_{0}+f_{1}+f_{2}+\cdots +f_{n}=f_{n+2}-1$

• Otras identidades interesantes incluyen las siguientes:

$f_{0}-f_{1}+f_{2}-\cdots +(-1)^{n}f_{n}=(-1)^{n}f_{n-1}-1$

$f_{1}+f_{3}+f_{5}+\cdots +f_{2n-1}=f_{2n}$

$f_{0}+f_{2}+f_{4}+\cdots +f_{2n}=f_{2n+1}-1$

$f_{0}^{2}+f_{1}^{2}+f_{2}^{2}+\cdots +f_{n}^{2}=f_{n}f_{n+1}$

$f_{1}f_{2}+f_{2}f_{3}+f_{3}f_{4}+\cdots +f_{2n-1}f_{2n}=f_{2n}^{2}$

$f_{1}f_{2}+f_{2}f_{3}+f_{3}f_{4}+\cdots +f_{2n}f_{2n+1}=f_{2n+1}^{2}-1$

Si $k\geq 1$, entonces $f_{n+k}=f_{k}f_{n+1}+f_{k-1}f_{n}\,$ para cualquier $n\geq 0$

$f_{n+1}f_{n-1}-f_{n}^{2}=(-1)^{n}$ (Identidad de Cassini)

$f_{n+1}^{2}+f_{n}^{2}=f_{2n+1}$

$f_{n+2}^{2}-f_{n+1}^{2}=f_{n}f_{n+3}$

$f_{n+2}^{2}-f_{n}^{2}=f_{2n+2}$

$f_{n+2}^{3}+f_{n+1}^{3}-f_{n}^{3}=f_{3n+3}$

• El máximo común divisor de dos números de Fibonacci es otro número de Fibonacci. Más específicamente

$\mathrm {mcd} \left(f_{n},f_{m}\right)=f_{\mathrm {mcd} \left(n,m\right)}$

Esto significa que $f_{n}\,$ y $f_{n+1}\,$ son primos relativos y que $f_{k}\,$ divide exactamente a $f_{nk}\,$

• Los números de Fibonacci aparecen al sumar las diagonales del triángulo de Pascal. Es decir que para cualquier $n\geq 0$,

$f_{n+1}=\sum _{j=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\begin{pmatrix}n-j\\j\end{pmatrix}}$

y más aún

$f_{3n}=\sum _{j=0}^{n}{\begin{pmatrix}n\\j\end{pmatrix}}2^{j}f_{j}$

• Si $f_{p}=a$, tal que $a$ es un número primo, entonces $p$ también es un número primo, con una única excepción, $f_{4}=3$; 3 es un número primo, pero 4 no lo es.
• La suma infinita de los términos de la sucesión $\textstyle {\frac {f_{n}}{10^{n}}}$ es exactamente $\textstyle {\frac {10}{89}}$.
• La suma de diez números Fibonacci consecutivos es siempre 11 veces superior al séptimo número de la serie.
• El último dígito de cada número se repite periódicamente cada 60 números. Los dos últimos, cada 300; a partir de ahí, se repiten cada $15\times 10^{n-1}$ números.

Generalización

Gráfica de la sucesión de Fibonacci extendida al campo de los números reales.

El concepto fundamental de la sucesión de Fibonacci es que cada elemento es la suma de los dos anteriores. En este sentido la sucesión puede expandirse al conjunto de los números enteros como $\ldots ,-8,5,-3,2,-1,1,0,1,1,2,3,5,8,\ldots$ de manera que la suma de cualesquiera dos números consecutivos es el inmediato siguiente. Para poder definir los índices negativos de la sucesión, se despeja $f_{n-2}\,$ de la ecuación (3) de donde se obtiene

$f_{n-2}=f_{n}-f_{n-1}\,$

De esta manera, $f_{-n}=f_{n}\,$ si $n$ es impar y $f_{-n}=-f_{n}\,$ si $n$ es par.

La sucesión se puede expandir al campo de los números reales tomando la parte real de la fórmula explícita (ecuación (6)) cuando $n$ es cualquier número real. La función resultante

$f(x)={\frac {\varphi ^{x}-\cos(\pi x)\varphi ^{-x}}{\sqrt {5}}}$

tiene las mismas características que la sucesión de Fibonacci:

• $f(0)=0~$
• $f(1)=1~$
• $f(x)=f(x-1)+f(x-2)~$ para cualquier número real $x$

Una sucesión de Fibonacci generalizada es una sucesión $g_{0},g_{1},g_{2},\ldots$ donde

(9)$g_{n}=g_{n-1}+g_{n-2}\,$ para $n=2,3,4,5,\ldots$

Es decir, cada elemento de una sucesión de Fibonacci generalizada es la suma de los dos anteriores, pero no necesariamente comienza en 0 y 1.

Una característica notable es que, si $g_{0},g_{1},g_{2},\ldots$ es una sucesión de Fibonacci generalizada, entonces

$g_{n}=f_{n-1}g_{0}+f_{n}g_{1}~$

Por ejemplo, la ecuación (7) puede generalizarse a

${\begin{bmatrix}0&1\\1&1\end{bmatrix}}^{n}{\begin{bmatrix}g_{0}\\g_{1}\end{bmatrix}}={\begin{bmatrix}g_{n}\\g_{n+1}\end{bmatrix}}$

Esto significa que cualquier cálculo sobre una sucesión de Fibonacci generalizada se puede efectuar usando números de Fibonacci.

Sucesión de Lucas

Gráfica de la sucesión de Lucas extendida al campo de los números reales

Un ejemplo de sucesión de Fibonacci generalizada es la sucesión de Lucas, descrita por las ecuaciones

• $l_{0}=2~$
• $l_{1}=1~$
• $l_{n}=l_{n-1}+l_{n-2}~$ para $n=2,3,4,5,\ldots$

La sucesión de Lucas tiene una gran similitud con la sucesión de Fibonacci y comparte muchas de sus características. Algunas propiedades interesantes incluyen:

• La proporción entre un número de Lucas y su sucesor inmediato se aproxima al número áureo. Es decir

$\lim _{n\to \infty }{\frac {l_{n+1}}{l_{n}}}=\varphi$

• La fórmula explícita para la sucesión de Lucas es

$l_{n}=\varphi ^{n}+(-\varphi )^{-n}$

• La suma de los primeros $n$ números de Lucas es el número que se encuentra en la posición $n+2$ menos uno. Es decir

$l_{0}+l_{1}+l_{2}+\cdots +l_{n}=l_{n+2}-1$

• Cualquier fórmula que contenga un número de Lucas puede expresarse en términos de números de Fibonacci mediante la igualdad

$l_{n}=f_{n-1}+f_{n+1}~$

• Cualquier fórmula que contenga un número de Fibonacci puede expresarse en términos de números de Lucas mediante la igualdad

$f_{n}={\frac {l_{n-1}+l_{n+1}}{5}}$

Algoritmos de cálculo

Para calcular el $n$-ésimo elemento de la sucesión de Fibonacci existen varios algoritmos (métodos). La definición misma puede emplearse como uno, aquí expresado en pseudocódigo:

Calculando $f_{7}$ usando el algoritmo 1

Algoritmo 1 Versión recursiva (Complejidad $O(\varphi ^{n})\,$)

función ${\it {fib}}(n)\,$ si $n<2\,$ entonces devuelva $n\,$ si no devuelva ${\it {fib}}(n-1)+{\it {fib}}(n-2)\,$

Usando técnicas de análisis de algoritmos es posible demostrar que, a pesar de su simplicidad, el algoritmo 1 requiere efectuar $f_{n+1}-1$ sumas para poder encontrar el resultado. Dado que la sucesión $f_{n}$ crece tan rápido como $\varphi ^{n}$, entonces el algoritmo está en el orden de $\varphi ^{n}$. Es decir, que este algoritmo es muy lento. Por ejemplo, para calcular $f_{50}$ este algoritmo requiere efectuar 20365011073 sumas.

Para evitar hacer tantas cuentas, es común recurrir a una calculadora y utilizar la ecuación (6), sin embargo, dado que $\varphi$ es un número irracional, la única manera de utilizar esta fórmula es utilizando una aproximación de $\varphi$ y obteniendo en consecuencia un resultado aproximado pero incorrecto. Por ejemplo, si se usa una calculadora de 10 dígitos, entonces la fórmula anterior arroja como resultado $f_{50}=1.258626903\times 10^{10}$ aun cuando el resultado correcto es $f_{50}=12586269025$. Este error se hace cada vez más grande conforme crece $n$.

Un método más práctico evitaría calcular las mismas sumas más de una vez. Considerando un par $(i,j)\,$ de números consecutivos de la sucesión de Fibonacci, el siguiente par de la sucesión es $(j,i+j)\,$, de esta manera se divisa un algoritmo donde sólo se requiere considerar dos números consecutivos de la sucesión de Fibonacci en cada paso. Este método es el que usaríamos normalmente para hacer el cálculo a lápiz y papel. El algoritmo se expresa en pseudocódigo como:

Algoritmo 2 Versión iterativa (Complejidad $O(n)\,$)

función ${\it {fib}}(n)\,$ $i\gets 1$ $j\gets 0$ para $k\,$ desde $1\,$ hasta $n\,$ haga $t\gets i+j$ $i\gets j$ $j\gets t$ devuelva $j\,$

Esta versión requiere efectuar sólo $n$ sumas para calcular $f_{n}$, lo cual significa que este método es considerablemente más rápido que el algoritmo 1. Por ejemplo, el algoritmo 2 sólo se requiere efectuar 50 sumas para calcular $f_{50}$.

Calculando $f_{100}$ usando el algoritmo 3

Un algoritmo todavía más rápido se sigue partiendo de la ecuación (8). Utilizando leyes de exponentes es posible calcular $x^{n}$ como

$x^{n}={\begin{cases}x&{\mbox{si }}n=1\\\left(x^{\frac {n}{2}}\right)^{2}&{\mbox{si }}n{\mbox{ es par}}\\x\times x^{n-1}&{\mbox{si }}n{\mbox{ es impar}}\end{cases}}$

De esta manera se divisa el algoritmo de tipo Divide y Vencerás donde sólo se requeriría hacer, aproximadamente, $\log _{2}(n)$ multiplicaciones matriciales. Sin embargo, no es necesario almacenar los cuatro valores de cada matriz dado que cada una tiene la forma

${\begin{bmatrix}a&b\\b&a+b\end{bmatrix}}$

De esta manera, cada matriz queda completamente representada por los valores $a$ y $b$, y su cuadrado se puede calcular como

${\begin{bmatrix}a&b\\b&a+b\end{bmatrix}}^{2}={\begin{bmatrix}a^{2}+b^{2}&b(2a+b)\\b(2a+b)&(a+b)^{2}+b^{2}\end{bmatrix}}$

Por lo tanto el algoritmo queda como sigue:

Algoritmo 3 Versión Divide y Vencerás (Complejidad $O(\log(n))\,$)

función ${\it {fib}}(n)\,$ si $n\leq 0$ entonces devuelva $0\,$ $i\gets n-1$ $(a,b)\gets (1,0)$ $(c,d)\gets (0,1)$ mientras $i>0\,$ haga si $i\,$ es impar entonces $(a,b)\gets (db+ca,d(b+a)+cb)$ $(c,d)\gets (c^{2}+d^{2},d(2c+d))$ $i\gets i\div 2$ devuelva $a+b\,$

A pesar de lo engorroso que parezca, este algoritmo permite reducir enormemente el número de operaciones que se necesitan para calcular números de Fibonacci muy grandes. Por ejemplo, para calcular $f_{100}$, en vez de hacer las 573147844013817084100 sumas del algoritmo 1 o las 100 sumas con el algoritmo 2, el cálculo se reduce a tan sólo 9 multiplicaciones matriciales.

La sucesión de Fibonacci, el número áureo y la sección áurea en la naturaleza

Para que las hojas esparcidas de una planta (Ver Filotaxis) o las ramas alrededor del tronco tengan el máximo de insolación con la mínima interferencia entre ellas, éstas deben crecer separadas en hélice ascendente según un ángulo constante y teóricamente igual a 360º (2 - φ) ≈ 137º 30' 27,950 580 136 276 726 855 462 662 132 999..." En la naturaleza se medirá un ángulo práctico de 137º 30' o de 137º 30' 28" en el mejor de los casos. Para el cálculo se considera iluminación vertical y el criterio matemático es que las proyecciones horizontales de unas sobre otras no se recubran exactamente. Aunque la iluminación del Sol no es, en general, vertical y varía con la latitud y las estaciones, esto garantiza el máximo aprovechamiento de la luz solar. Este hecho fue descubierto empíricamente por Church y confirmado matemáticamente por Weisner en 1875. La letra griega φ representa al número áureo, como se explica más arriba. En la práctica no puede medirse con tanta precisión el ángulo y las plantas lo reproducen "orgánicamente"; o sea, con un error pequeño, pero existente.

En la cantidad de elementos constituyentes de las espirales o dobles espirales de las inflorescencias, como en el caso del girasol, y en otros objetos orgánicos como las piñas de los pinos se encuentran números pertenecientes a la sucesión de Fibonacci.

La sucesión de Fibonacci en la cultura popular

• En la pág. 61 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el conservador del museo del Louvre, Jacques Saunière.
• En el álbum Lateralus de la banda estadounidense Tool, los patrones de la batería (Danny Carey) de la canción "Lateralus" siguen la Sucesión de Fibonacci del número 13 (número de pistas del disco): 1,1,2,3,5,8,13,1,1,2,3,5,8,13,1,1,...
• En la miniserie Abducidos, la Sucesión de Fibonacci, como la Ecuación de Dios, es descubierta en los planes de los extraterrestres, en ejemplos como que sus naves tienen 5 tripulantes, sus manos 3 dedos y un pulgar, 1597 avistamientos ovnis en año anterior, se siguieron a 55 parejas para descubrir la hibrida humano-extraterrestre Allie, y que finalmente el número de abducidos era de 46368. Incidentalmente se habla en de un hombre que fue abducido 13 veces. 1, 3, 5, 13, 55, 1597, 46368, todos números Fibonacci.
• En el filme de Darren Aronofsky π el orden del caos el judío Rabbi Cohen presenta la teoría en hebreo transcrito en números en la cual el personaje Max Cohen relaciona esta última teoría con la secuencia de Fibonacci llegando en conclusión que todo esta basado en la ley del orden y el caos.
• En un lateral de la cúpula de la antigua sinagoga ahora convertida en el Museo Nazionale del Cinema, más conocida como Mole Antonelliana, en Torino (Italia), se puede observar una instalación luminosa de la sucesión de números de Fibonacci.

Referencias

• Kolman, Bernard; Hill, David R. (2006). Álgebra Lineal. México: PEARSON EDUCACIÓN. ISBN 970-26-0696-9. 
• Johnsonbaugh, Richard (2005). Matemáticas Discretas. México: PEARSON EDUCACIÓN. ISBN 970-26-0637-3. 
• Brassard, G; Bratley, P. (1997). Fundamentos de Algoritmia. Madrid: PRETINCE HALL. ISBN 84-89660-00-X. 
• Kenneth, H. Rosen (2003). Discrete mathematics and its applications. McGraw Hill. ISBN 0-07-123374-1. 
• Kenneth H. Rosen; John G. Michaels (1999). Handbook of discrete and combinatorial mathematics. CRC. ISBN 0-8493-0149-1. 

• N. N. Vorobiov (1974). Números de Fibonacci. Editorial Mir, Moscú, Colección Lecciones Populares de Matemáticas. Traducción al español de Carlos Vega, catedrático de Matemáticas Superiores y candidato a doctor en ciencias físico-matemáticas. 

• A. I. Markushevich (1974; 1981). Sucesiones recurrentes. Editorial Mir, Moscú, Colección Lecciones Populares de Matemáticas. Traducción al español de Carlos Vega. 

• Luca Pacioli (1946). La Divina Proporción. Editorial Losada, Buenos Aires. 

Véase también

• Sucesión matemática
• Sistema-L
• Espiral logarítmica
• Arte Póvera, movimiento artístico italiano de los años sesenta, muchas de cuyas obras se basan en esta sucesión.
• Montículo de Fibonacci, estructura de datos en Informática.

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre números de Fibonacci.
• Fibonacci's Liber Abaci en libros de Google
• Sucesión de Fibonacci en Mathworld explicación muy detallada, en inglés.
• Diagrama de flujo de la serie o sucesión de Fibonacci
• Información en www.formación.cnice.mec.es

• Implementación en Pascal
• (pt) Veja como posicionar a sequência de fibonacci
• Implementación en Lexico