Distribución beta

En estadística, una variable aleatoria $X$ tiene una distribución beta con parámetros $\alpha ,\beta >0$ y escribimos $X\sim B(\alpha ,\beta )$ si y sólo si su función de densidad para valores $0<x<1$ es

Beta
Función de densidad de probabilidad
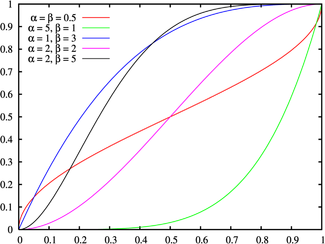
Función de distribución de probabilidad
Parámetros	$\alpha >0$ forma (real) $\beta >0$ forma (real)
Dominio	$x\in [0;1]\!$
Función de densidad (pdf)	${\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\!$
Función de distribución (cdf)	$I_{x}(\alpha ,\beta )\!$
Media	${\frac {\alpha }{\alpha +\beta }}\!$
Moda	${\frac {\alpha -1}{\alpha +\beta -2}}\!$ para $\alpha >1,\beta >1$
Varianza	${\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!$
Coeficiente de simetría	${\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}$
Función generadora de momentos (mgf)	$1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}$
Función característica	${}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!$

$f(x)={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{B(\alpha ,\beta )}}$

donde $B(\alpha ,\beta )$ es la función beta y se define para $\alpha ,\beta >0$ como

$B(\alpha ,\beta )=\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx$

y satisface

1. $B(\alpha ,\beta )=B(\beta ,\alpha )$
2. $B(\alpha ,\beta )={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}$

El valor esperado y la varianza de una variable aleatoria $X\sim B(\alpha ,\beta )$ son

${\text{E}}[X]={\frac {\alpha }{\alpha +\beta }}$

${\text{Var}}[X]={\frac {\alpha \beta }{(\alpha +\beta +1)(\alpha +\beta )^{2}}}$.

Un caso especial de la distribución beta es cuando $\alpha =1$ y $\beta =1$ que coincide con la distribución uniforme en el intervalo [0, 1].

Animación de la función de densidad de la distribución Beta para diferentes valores de sus parámetros

• Datos: Q756254
• Multimedia: Beta distribution