Homomorfismo de grupos

En álgebra, un homomorfismo de grupos es una función entre grupos que preserva la operación binaria.

Imagen de un homomorfismo de grupos (h) de G(izquierda) en H(derecha). El óvalo menor dentro de H es la imagen de h. N es el núcleo de h y aN es una clase lateral de N.

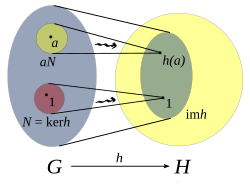
Dados dos grupos $(G,\circ )$ y $(H,\ast )$ la aplicación $\quad \varphi :G\longrightarrow H\quad$ es un homomorfismo de grupos si se verifica que para todos los pares de elementos $a,b\in G$

$\varphi (a\circ b)=\varphi (a)\ast \varphi (b)$

donde la operación en el lado izquierdo de la ecuación ($\circ$) es la ley de composición interna en $G$, y la operación del lado derecho de la ecuación ($\ast$) es la ley de composición interna en $H$.​

Si la aplicación $\varphi$ es biyectiva entonces es un isomorfismo de grupos, lo que significa que ambos grupos tienen la misma estructura algebraica (son isomorfos), y sólo se diferencian por los símbolos utilizados para denotar los elementos y la operación.

Definiciones

Dados dos grupos $(G,\circ )$ y $(H,\ast )$, en el que cada grupo está compuesto por un conjunto de elementos y una ley de composición interna entre ellos (no necesariamente la misma), es posible definir una función que asigne a cada elemento g de $G$ un elemento h de $H$:

$\quad \varphi :G\longrightarrow H\quad$

Dicha función es un homomorfismo de grupos si se verifica que para todos los pares de elementos $a,b\in G$

$\varphi (a\circ b)=\varphi (a)\ast \varphi (b)$

donde la operación en el lado izquierdo de la ecuación ($\circ$) es la ley de composición interna en $G$, y la operación del lado derecho de la ecuación ($\ast$) es la ley de composición interna en $H$.​

Imagen de $\varphi$

El conjunto de todos los elementos de $H$ que son la imagen de algún elemento de $G$ se llama la imagen de la aplicación, y se denota ${\rm {{Im}(\varphi )}}$ o $\varphi (G)$.​ Formalmente:

${\rm {{Im}(\varphi ):\lbrace h\in H:h=\varphi (g),\ para\ alg{\acute {u}}n\ g\in G\rbrace }}$

La imagen de $\varphi$ es un subgrupo de $H$.

El núcleo o kernel

El conjunto de todos los elementos de $G$ cuya imagen es el elemento identidad de $H$ se llama núcleo (kernel) de $\varphi$:

$\ker(\varphi ):\lbrace g\in G:\varphi (g)=1_{H}\rbrace$

El núcleo de $\varphi$ es un subgrupo normal de G. El núcleo es importante porque no sólo determina qué elementos tienen por imagen la identidad, sino también qué elementos tienen la misma imagen:​

Dado $a\in G\rightarrow \varphi (a\circ k)=\varphi (a)\qquad \forall k\in \ker(\varphi )$

ya que $\varphi (a\circ k)=\varphi (a)\ast \varphi (k)=\varphi (a)\ast 1_{H}=\varphi (a)$

Los conjuntos de todos los elementos que comparten una misma imagen son las clases laterales del núcleo.

Ejemplos

La función exponencial es un homomorfismo de grupos entre los números reales bajo la adición y el grupo multiplicativo de los reales no nulos (excluido el 0):

$f:(\mathbb {R} ,+)\longrightarrow (\mathbb {R} ^{\ast },\cdot )\quad tal\ que\ f(x)=e^{x}$

dado que $\quad f(x+y)=e^{x+y}=e^{x}\ e^{y}=f(x)\cdot f(y)$

La imagen de la función exponencial es el subgrupo de los números reales positivos, y el núcleo es solo el elemento identidad (el 0), ya que la aplicación es inyectiva.

La función determinante, definida sobre el grupo multiplicativo de matrices invertibles (grupo general lineal) en los números reales no nulos, es un homomorfismo de grupos:

$f:\mathbb {GL} _{n}(\mathbb {R} )\longrightarrow (\mathbb {R} ^{\ast },\cdot )\quad tal\ que\ f(A)=det(A)$

dado que $\quad \det(A\times B)=\det(A)\cdot \det(B)$.

Tipos de homomorfismos

• un monomorfismo de grupos es un homomorfismo de grupos inyectivo, aquel en el que no hay dos elementos de $G$ con la misma imagen:

$\forall g_{1},g_{2}\in G:\varphi (g_{1})=\varphi (g_{2})\iff g_{1}=g_{2}$

El núcleo de un monomorfismo sólo contiene al elemento identidad, y a la inversa, cuando el núcleo sólo contiene al elemento identidad entonces la función es un monomorfismo.

• un epimorfismo de grupos es un homomorfismo de grupos sobreyectivo, aquel en el que todo elemento de $H$ es imagen de algún elemento de $G$. Bajo estas condiciones, la imagen de $\varphi$ es todo $H$:

$\forall h\in H:h=\varphi (g),\ para\ alg{\acute {u}}n\ g\in G$

• un isomorfismo de grupos es un homomorfismo de grupos que es simultáneamente inyectivo y sobreyectivo, o lo que es lo mismo, biyectivo. cuando esto ocurre, ambos grupos tienen la misma estructura algebraica (son isomorfos), y sólo se diferencian por los símbolos utilizados para denotar al conjunto, los elementos y la operación.
• un endomorfismo es un homomorfismo de un grupo en sí mismo:

$\quad \varphi :G\longrightarrow G\quad$.

• un automorfismo es un endomorfismo biyectivo. Nótese que, en un grupo finito, cuando un endomorfismo es inyectivo entonces es sobreyectivo, y viceversa. El conjunto de todos los automorfismos de un grupo G, con la composición de funciones como operación, es en sí mismo un grupo llamado grupo de automorfismos de G (Aut(G)). Como ejemplo, el grupo de automorfismos de $(\mathbb {Z} ,+)$ sólo contiene dos elementos: la transformación identidad [f(n)=n] y la multiplicación por -1 [f(n)=-n], por lo que es isomorfo a $\mathbb {Z} /2\mathbb {Z}$.

Propiedades

Dado un homomorfismo de grupos $\quad \varphi :G\longrightarrow H\quad$, se verifican las siguientes propiedades:

• La imagen del elemento identidad de $G$ es el elemento identidad de $H$:$\varphi (1_{G})=1_{H}$.

Demostración

Por ser $1_{G}$ la identidad: $1_{G}=1_{G}\circ 1_{G}$ Por ser $\varphi$ un homomorfismo: $\varphi (1_{G})=\varphi (1_{G})\ast \varphi (1_{G})$ Multiplicando por $\varphi (1_{G})^{-1}$: $\varphi (1_{G})\ast \varphi (1_{G})^{-1}=\varphi (1_{G})\ast \varphi (1_{G})\ast \varphi (1_{G})^{-1}$ Simplificando: $1_{H}=\varphi (1_{G})\ast 1_{H}=\varphi (1_{G})$.

• El núcleo de $\varphi$ es un subconjunto no vacío:$\ker(\varphi )\neq \varnothing$.

Demostración

Por el resultado anterior $1_{G}\in \ker(\varphi )$, así que el núcleo contiene como mínimo al elemento identidad.

• La imagen de un inverso es el inverso de la imagen: $\varphi (a^{-1})=\varphi (a)^{-1}$.

Demostración

Aplicando las propiedades obtenidas hasta ahora: $1_{H}=\varphi (1_{G})=\varphi (a\circ a^{-1})=\varphi (a)\ast \varphi (a^{-1})$ y dado que los elemento inversos son únicos: $\varphi (a^{-1})=\varphi (a)^{-1}$.

• Si $G'$ es un subgrupo de $G$, su imagen $H'$ es un subgrupo de $H$.

Demostración

Veamos que se cumplen las siguientes propiedades: $H'$ es cerrado bajo la operación del grupo: $\forall \varphi (g_{1}),\varphi (g_{2})\in H',\ donde\ g_{1},g_{2}\in G':$ $\varphi (g_{1})\ast \varphi (g_{2})=\varphi (g_{1}\circ g_{2})\in H'$ Contiene la identidad: $1_{G}\in G'\Rightarrow 1_{H}=\varphi (1_{G})\in H'$ Contiene los inversos: $\forall \varphi (g)\in H',\ donde\ g\in G;\varphi (g)^{-1}=\varphi (g^{-1})\in H'$

• Si $H'$ es un subgrupo de $H$, su preimagen $G'$ es un subgrupo de $G$.

Demostración

Veamos que se cumplen las siguientes propiedades: $G'$ es cerrado bajo la operación del grupo: $\forall g_{1},g_{2}\in G'\ donde\ \varphi (g_{1}),\varphi (g_{2})\in H':$ $\varphi (g_{1}\circ g_{2})=(\varphi (g_{1})\ast \varphi (g_{2}))\in H'\Rightarrow g_{1}\circ g_{2}\in G'$ Contiene la identidad: $1_{H}=\varphi (1_{G})\Rightarrow 1_{G}\in G'$ Contiene los inversos: $\forall g\in G';\ \varphi (g^{-1})=\varphi (g)^{-1}\in H'\Rightarrow g^{-1}\in G'$

• Continuando lo anterior, si $H'$ es normal en $H$, entonces su preimagen $G'$ es normal en $G$:​

Demostración

Para demostrar que $G'$ es normal en $G$ se debe cumplir que $\forall g\in G\Rightarrow (g^{-1}\circ G'\circ g)\in G'$ pero $\forall g'\in G'\Rightarrow \varphi (g^{-1}\circ g'\circ g)=(\varphi (g)^{-1}\ast \varphi (g')\ast \varphi (g))\in H'$ dado que $H'$ es normal en $H$.

• El núcleo de un homomorfismo es un subgrupo normal de $G$:$\ker(\varphi )\vartriangleleft G$.

Demostración

Primero veamos que es un subgrupo: El núcleo de $\varphi$ es cerrado: para todo $a,b\in \ker(\varphi )\Rightarrow \varphi (a\circ b)=\varphi (a)\ast \varphi (b)=1_{H}\ast 1_{H}=1_{H}$ Contiene al elemento identidad: $\varphi (1_{G})=1_{H}$, como ya se demostró antes. Contiene los inversos: para todo $a\in \ker(\varphi )\Rightarrow \varphi (a^{-1})=\varphi (a)^{-1}=(1_{H})^{-1}=1_{H}$ Además, es un subgrupo normal en $G$ porque es la preimagen de $1_{H}$ (el subgrupo trivial de $H$), que es normal en $H$.

• La imagen de $\varphi$ es un subgrupo de $H$: ${\rm {{im}(\varphi )\leq H}}$.

Demostración

Veamos que se cumplen las siguientes propiedades: La imagen de $\varphi$ es cerrada: $\forall a,b\in G\Rightarrow \varphi (a)\ast \varphi (b)=\varphi (a\circ b)\in {\rm {{im}(\varphi )}}$. Contiene al elemento identidad: $\varphi (1_{G})=1_{H}\Rightarrow 1_{H}\in {\rm {{im}(\varphi )}}$ Contiene los inversos: $\forall a\in G\Rightarrow \varphi (a)^{-1}=\varphi (a^{-1})\in {\rm {{im}(\varphi )}}$

Teoremas fundamental y de isomorfía

El teorema fundamental expresado como un diagrama conmutativo.

Teorema fundamental

Sean $f:G\longrightarrow H$ un homomorfismo de grupos y $N$ un subgrupo normal de $G$ contenido en el núcleo de $f$, entonces existe un único homomorfismo ${\bar {f}}$ tal que ${\bar {f}}\circ \varphi =f$, en donde $\varphi :G\longrightarrow G/N$ es la proyección canónica y $G/N$ es un grupo cociente.​

Teoremas de isomorfismo

• El primera teorema es un caso particular del teorema fundamental:

Sea $f:G\longrightarrow H$ un homomorfismo de grupos. Entonces existe un isomorfismo ${\bar {f}}:G/(\ker f)\longrightarrow \mathrm {im} \ f$, y por tanto $G/(\ker f)\cong \mathrm {im} \ f.$

• Segundo teorema:

Si $N$ y $H$ son subgrupos de un grupo $G$, con $N$ normal en $G$, entonces $NH$ es un subgrupo de $G$, $H\cap N$ es normal en $G$ y $H/(H\cap N)\cong (HN)/N.$

• Tercer teorema:

Si $N$ y $H$ son subgrupos normales de un grupo $G$, con $N\subseteq H$, entonces $G/H\cong (G/N)/(H/N).$

Véase también

• Homomorfismo.
• Grupo (matemática).
• Teoría de grupos.
• Teoremas de isomorfía.
• Acción de grupo.

Referencias

Bibliografía

• Judson, Thomas W. (2012). Abstract Algebra. Theory and Applications (pdf). disponible online bajo licencia GFDL. 
• Artin, Michael (2011). Algebra (2ª edición). Pearson Education. ISBN 978-0132413770. 

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Homomorfismo de grupos.
• Wikilibros alberga un libro o manual sobre Homomorfismo de grupos.
• Weisstein, Eric W. «Group Homomorphism». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Group homomorphism en PlanetMath.

• Datos: Q868169
• Multimedia: Group homomorphisms / Q868169