Triángulo entero
Un triángulo entero (también denominado en ocasiones triángulo integral) se caracteriza porque sus lados tienen longitudes que son números enteros.
Un triángulo racional se puede definir como uno que tiene todos los lados con longitud racional, si bien cualquier triángulo racional de este tipo se puede volver a escalar (puede tener todos los lados multiplicados por el mismo entero, es decir, un múltiplo común de sus denominadores) para obtener un triángulo entero, por lo que no hay diferencia sustancial entre triángulos enteros y triángulos racionales en este sentido.
Sin embargo, debe tenerse en cuenta que también existen otras definiciones del término "triángulo racional": en 1914, Carmichael[1] utilizó el término en el sentido en que hoy se usa el término de triángulo heroniano; Somos[2] lo usa para referirse a triángulos cuyas proporciones entre sus lados son racionales; Conway y Guy[3] definen un triángulo racional como uno con lados racionales y ángulos racionales medidos en grados, en cuyo caso el único triángulo racional es el triángulo equilátero de lado racional.
Los triángulos enteros poseen varias propiedades generales, explicadas en la primera sección que figura a continuación. Todas las demás secciones se refieren a clases de triángulos enteros con propiedades específicas.
Propiedades generales para un triángulo entero
editarTriángulos enteros con el perímetro dado
editarTres enteros positivos cualesquiera pueden servir como longitudes laterales de un triángulo entero, siempre que satisfagan la desigualdad del triángulo: el lado más largo es más corto que la suma de los otros dos lados. Cada una de estas ternas de números define un triángulo entero que es único (descontadas congruencias). Entonces el número de triángulos enteros (descontando triángulos congruentes; es decir, aquellos con las mismas longitudes pero con distinta ordenación) con el perímetro p es el número de particiones de p en tres partes positivas que satisfacen la desigualdad del triángulo. Este es el número entero más cercano a p2⁄48 cuando p es par y para (p + 3)2⁄48 cuando p es impar.[4][5] También significa que el número de triángulos enteros con perímetros de número par p = 2n es la misma que la cantidad de triángulos enteros con perímetros impares p = 2n - 3 (ambas cantidades dependen linealmente de n). Por lo tanto, no hay un triángulo entero con el perímetro 1, 2 o 4; solo uno con el perímetro 3, 5, 6 u 8; y dos con el perímetro 7 o 10. La secuencia del número de triángulos enteros con el perímetro p, comenzando en p = 1, es:
Triángulos enteros con el lado más grande dado
editarEs posible determinar el número de triángulos enteros (sin contar congruencias) con el lado más grande dado c y el triplete de números enteros (a, b, c) tal que a + b > c y a ≤ b ≤ c. Este número de triángulos enteros se calcula como Techo [(c + 1)⁄2] * Suelo [(c + 1)⁄2].[4] Alternativamente, para c par es el doble número triangular c⁄2 (c⁄2 + 1) y para c impar es el cuadrado (c + 1)2⁄4. Esto también significa que el número de triángulos enteros con el lado más grande c excede el número de triángulos enteros con el lado más grande c−2 por c. La secuencia del número de triángulos enteros no congruentes con el lado más grande c, que comienza en c = 1, es:
El número de triángulos enteros (sin congruencia) con el lado más grande dado c y la tripleta de números enteros (a, b, c) que se encuentran en o dentro de un semicírculo de diámetro c es el número de triples enteros tal que a + b > c , a2 + b2 ≤ c2 y a ≤ b ≤ c. Este es también el número de triángulos enteros obtusos o rectángulos (no agudos) con el lado más grande c. La secuencia que comienza en c = 1, es:
En consecuencia, la diferencia entre las dos secuencias anteriores da la cantidad de triángulos enteros agudos (sin congruencia) con el lado más grande dado c. La secuencia que comienza en c = 1, es:
Área de un triángulo entero
editarPor la fórmula de Herón, si T es el área de un triángulo cuyos lados tienen longitudes a, b y c, entonces
Dado que todos los términos bajo la raíz en el lado derecho de la fórmula son enteros, se deduce que el área T de cualquier triángulo entero cumple que 16T2 es también un número entero, y que T2 es un número racional.
Ángulos de un triángulo entero
editarPor el teorema del coseno, cada ángulo de un triángulo entero tiene un coseno que es un número racional.
Si los ángulos de cualquier triángulo forman una progresión aritmética, entonces uno de sus ángulos debe ser 60°.[6] Para triángulos enteros, los ángulos restantes también deben tener cosenos racionales y a continuación se proporciona un método para generar dichos triángulos. Sin embargo, aparte del caso trivial de un triángulo equilátero, no hay triángulos enteros cuyos ángulos formen una progresión geométrica o armónica. Esto se debe a que dichos ángulos deben ser ángulos racionales de la forma πp⁄q con 0 < p⁄q < 1. Pero todos los ángulos de un triángulo entero deben tener cosenos racionales y esto debe ocurrir solo cuando p⁄q = 1⁄3 [7]: p.2 es decir, cuando el triángulo entero es equilátero.
El cuadrado de la longitud de cada segmento de bisectriz situado dentro de un triángulo entero es un número racional, porque la fórmula general del triángulo para la longitud del segmento de bisectriz del ángulo interno A es , donde s es el semiperímetro (y lo mismo para las bisectrices de los otros dos ángulos).
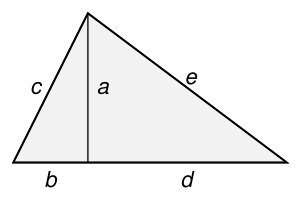
Lado dividido por una altura
editarCualquier altura trazada desde un vértice sobre su lado opuesto o la extensión de este, dividirá ese lado o su extensión en longitudes que serán números racionales.
Medianas
editarEl cuadrado de dos veces la longitud de cualquier mediana de un triángulo entero es un número entero, porque la fórmula general para el largo de la mediana ma2 del lado a es , dando (2ma)2 = 2b2 + 2c2 − a2 (y lo mismo para las medianas de los otros lados).
Circunradios e inradios
editarComo el cuadrado del área de un triángulo entero es racional, el cuadrado de su circunradio también es racional, al igual que el cuadrado de su inradio.
La relación entre el inradio y el circunradio de un triángulo entero es racional, lo que equivale a para el semiperímetro s y el área T.
El producto del inradio y el circunradio de un triángulo entero es racional, lo que equivale a
Por lo tanto, el cuadrado de la distancia entre el incentro y el circuncentro de un triángulo entero, dada por el teorema de Euler como R2−2Rr, es racional.
Triángulos heronianos
editarFórmula general
editarUn triángulo heroniano, también conocido como triángulo de Herón, es un triángulo con lados enteros y área entera. Cada triángulo heroniano tiene lados proporcionales a[8]
para los enteros m, n y k sujetos a las restricciones:
- .
El factor de proporcionalidad generalmente es un número racional , donde reduce el triángulo heroniano generado a su primitivo y escala este primitivo al tamaño requerido.
Triángulos pitagóricos
editarUn triángulo pitagórico tiene un ángulo recto y es heroniano. Sus tres lados enteros se conocen como terna pitagórica, triplete pitagórico' o tríada pitagórica[9] Todo triplete pitagórico con hipotenusa primitiva (es decir, que los lados no tienen factor común con ella), puede ser generado por
donde m y n son enteros números primos entre sí y uno de ellos es par con m > n.
Cada número par mayor que 2 puede ser la pata de un triángulo pitagórico (no necesariamente primitivo) porque si la pata está dada por y se elige como la otra pata, entonces la hipotenusa es .[10] Esta es esencialmente la fórmula de generación anterior con fijado en el valor 1, y permite que varíe de 2 a infinito.
Triángulos pitagóricos con la altura de la hipotenusa entera
editarNo hay triángulos pitagóricos primitivos con una altura entera a partir de la hipotenusa. Esto es porque dos veces el área es igual a cualquier base multiplicada por la altura correspondiente: 2 veces el área equivale tanto a ab como a cd, donde d es la altura de la hipotenusa c. Las tres longitudes de los lados de un triángulo primitivo son coprimas, por lo que d = ab⁄c está en forma completamente reducida; como c no puede ser igual a 1 para cualquier triángulo pitagórico primitivo, d no puede ser un número entero.
Sin embargo, cualquier triángulo pitagórico con patas x e y; e hipotenusa z, puede generar un triángulo pitagórico con una altura entera, escalando los lados por la longitud de la hipotenusa z. Si d es la altura, entonces el triángulo pitagórico generado con la altura entera viene dado por[11]
En consecuencia, todos los triángulos pitagóricos con las patas a y b, hipotenusa c, y la altura entera de la hipotenusa d, con gcd (a, b, c, d) = 1, que necesariamente tienen ambos a2 + b2 = c2 y , son generados por[12][11]
para los números enteros coprimos m, n con m > n.
Triángulos heronianos con lados en progresión aritmética
editarUn triángulo con lados enteros y área entera tiene lados en progresión aritmética si y solo si[13] los lados son (b - d, b, b + d ), donde
y donde g es el máximo común divisor de y
Triángulos heronianos con un ángulo igual a dos veces otro
editarTodos los triángulos Heronianos con la relación entre ángulos B = 2A, son generados por[14]
con enteros k, s y r tales que s2 > 3r2, o
- ,
- ,
- ,
- ,
con enteros q, u y v tales que v > u; y v2 < (7+4√3) u2.
Ningún triángulo heroniano con B = 2A es isósceles o un triángulo rectángulo, porque todas las combinaciones resultantes generan ángulos con senos no racionales, dando un área o un lado no racional.
Triángulos heronianos isósceles
editarTodos los triángulos isósceles heronianos son descomponibles. Se forman uniendo dos triángulos pitagóricos congruentes en cualquiera de sus catetos comunes, de modo que los lados iguales del triángulo isósceles son las hipotenusas de los triángulos pitagóricos, y la base del triángulo isósceles es el doble del otro cateto del triángulo pitagórico. En consecuencia, cada triángulo pitagórico sirve como bloque de construcción de dos triángulos heronianos isósceles, ya que la unión puede ser en cualquiera de sus dos catetos. Todos los pares de triángulos heronianos isósceles están dados por múltiplos racionales de[15]
y
para los números enteros coprimos u y v, con u > v y u + v impar.
Triángulos heronianos cuyo perímetro es cuatro veces un primo
editarSe ha demostrado que un triángulo heroniano cuyo perímetro es cuatro veces un número primo está asociado de manera única con el primo y que el primo tiene la forma .[16][17] Es bien sabido que un número primo puede dividirse de manera única en enteros y de modo que (véase números idóneos de Euler). Además, se ha demostrado que tales triángulos heronianos son primitivos, ya que el lado más pequeño del triángulo tiene que ser igual al primo que es un cuarto de su perímetro.
En consecuencia, todos los triángulos heronianos primitivos cuyo perímetro es cuatro veces un primo pueden ser generado por
para los enteros y de modo que sea un primo.
Además, la factorización del área es , donde es primo. Sin embargo, el área de un triángulo heroniano siempre es divisible por . Esto da como resultado que, aparte de y que dan , todas las demás separaciones de y deben tener impar con solo una de ellas divisible por .
Triángulos heronianos con inradio y exradios enteros
editarHay infinidad de triángulos heronianos (no pitagóricos) primitivos (descomponibles e indescomponibles), con radios enteros de su incírculo y de cada uno de sus tres excírculos.[18]: Thms. 3 y 4 Una familia de triángulos heronianos descomponibles viene dada por
y una familia de indescomponibles viene dada por
Triángulos heronianos como caras de un tetraedro
editarExisten tetraedros cuyo volumen es un valor entero, y triángulos de Herón como caras. Un ejemplo tiene una arista de longitud 896, la arista opuesta de 190, y los otros cuatro bordes de 1073; dos caras tienen áreas de 436.800 y las otras dos tienen áreas de 47.120, mientras que su volumen es de 62.092.800.[19]: p.107
Triángulos enteros automedianos
editarUn triángulo automediano es aquel cuyas medianas están en las mismas proporciones (en el orden opuesto) que los lados. Si x, y, y z son los tres lados de un triángulo rectángulo, ordenados en orden creciente por tamaño, y si 2x < z, entonces z, x + y, e y − x son los tres lados de un triángulo automediano. Por ejemplo, el triángulo rectángulo con lados 5, 12 y 13 puede usarse de esta manera para formar el triángulo automediano entero más pequeño, con longitudes de lados 13, 17 y 7.[20] En consecuencia, utilizando la fórmula de Euclides, que genera triángulos pitagóricos primitivos, es posible generar triángulos automedianos enteros primitivos como
con y coprimos; impar; y o , que satisfaga la desigualdad triangular.
Triángulos enteros en una retícula bidimensional
editarUna retícula bidimensional es una matriz regular de puntos aislados, donde si se elige un punto como origen cartesiano (0, 0), entonces todos los otros puntos están en coordenadas (x, y), donde x e y, con alcance sobre todos los enteros positivos y negativos. Un triángulo reticular es cualquier triángulo dibujado dentro de una retícula bidimensional, tal que todos sus vértices se encuentran en puntos de la retícula. Por el teorema de Pick, un triángulo reticular tiene un área racional que, o bien es un número entero o tiene un denominador de 2. Si el triángulo reticulado tiene lados enteros, entonces es heroniano con un área entera.[21]
Además, se ha demostrado que todos los triángulos heronianos se pueden dibujar como triángulos reticulares.[22][23] Por consiguiente, un triángulo entero es heroniano si y solo si se puede dibujar como un triángulo reticular.
Hay infinitos triángulos heronianos (no pitagóricos) primitivos que se pueden colocar sobre una retícula entera, incluidos todos sus vértices, el incentro y los tres excentros. Dos familias de tales triángulos son las que tienen las parametrizaciones dadas anteriormente en Triángulos heronianos con inradio y exradios enteros.[18]: Thm. 5
Triángulos enteros con propiedades angulares específicas
editarTriángulos enteros con una bisectriz racional
editarUna familia de triángulos con lados enteros y con una bisectriz racional de ángulo A, viene dada por[24]
con enteros .
Triángulos enteros con nsectrices enteras
editarExisten infinitos triángulos no similares en los que los tres lados y las bisectrices de cada uno de los tres ángulos son enteros.[25]
Existen infinitos triángulos no similares en los que los tres lados y los dos trisectores de cada uno de los tres ángulos son enteros.[25]
Sin embargo, para n > 3 no existen triángulos en los que los tres lados y los (n - 1) nsectores de cada uno de los tres ángulos sean enteros.[25]
Triángulos enteros con un ángulo con un coseno racional dado
editarAlgunos triángulos enteros con un ángulo en el vértice A dado el coseno racional h/k (h < 0 o > 0; k > 0) están definidos por[26]
donde p y q son los enteros positivos coprimos tales que p > qk.
Triángulos enteros con un ángulo de 60° (ángulos en progresión aritmética)
editarTodos los triángulos enteros con un ángulo de 60° tienen sus ángulos en una progresión aritmética. Todos los triángulos son proporcionales a:[6]
con enteros coprimos m, n y 1 ≤ n ≤ m o 3m ≤ n. A partir de aquí, todas las soluciones primitivas se pueden obtener dividiendo a, b y c por su máximo común divisor.
Los triángulos enteros con un ángulo de 60° también pueden ser generados por[27]
con enteros coprimos m, n con 0 < n < m (el ángulo de 60° es opuesto al lado de longitud a). A partir de aquí, todas las soluciones primitivas pueden ser obtenidas dividiendo a, b y c por su máximo común divisor (por ejemplo, una solución al triángulo equilátero se obtiene tomando m = 2 y n = 1, pero esto produce a = b = c = 3, que no es una solución primitiva). Véase también[28][29]
Más precisamente, si , entonces , de lo contrario . Dos pares diferentes y generan el mismo triplete. Desafortunadamente, los dos pares pueden ser ambos de mcd = 3, por lo que no se pueden evitar los duplicados simplemente omitiendo ese caso. En cambio, los duplicados se pueden evitar con solo hasta . Téngase en cuenta que todavía se necesita dividir por 3 si el mcd = 3. La única solución para bajo las restricciones anteriores es para . Con esta restricción adicional, todas las tripletas se pueden generar de forma única.
Una terna de Eisenstein es un conjunto de enteros que son las longitudes de los lados de un triángulo donde uno de los ángulos es de 60 grados.
Triángulos enteros con un ángulo de 120°
editarLos triángulos enteros con un ángulo de 120° pueden ser generados por[30]
con enteros coprimos m, n con 0 < n < m (el ángulo de 120° es opuesto al lado de longitud a). A partir de aquí, todas las soluciones primitivas pueden obtenerse dividiendo a, b, y c por su máximo común divisor (por ejemplo, tomando m = 4 y n = 1, se obtiene a = 21, b = 9 y c = 15, que no es una solución primitiva, pero que lleva a la solución primitiva a = 7, b = 3, y c = 5, que en orden creciente, puede obtenerse con los valores m = 2 y n = 1).[28][29]
Más precisamente, si , entonces , de lo contrario . Como el lado más grande a solo se puede generar con un solo par , cada triplete primitivo se puede generar de dos maneras: una directamente con mcd = 1 y una indirectamente con mcd = 3. Por lo tanto, para generar todas las tripletas primitivas de manera única, se puede agregar la condición adicional de que .
Triángulos enteros con un ángulo igual a un número racional arbitrario de veces otro ángulo
editarPara enteros primos relativos positivos h y k, el triángulo con los siguientes lados tiene ángulos , y y, por lo tanto, dos ángulos en la relación h:k, y sus lados son enteros:[31]
donde y p y q son números primos relativos tales que .
Triángulos enteros con un ángulo igual a dos veces otro
editarCon el ángulo A opuesto al lado y el ángulo B opuesto al lado , algunos triángulos con B = 2A son generados por[32]
con enteros m y n, tales que 0 < n < m < 2n.
Nótese que todos los triángulos con B = 2A (siendo entero o no) tienen[33] .
Triángulos enteros con un ángulo igual a 3/2 veces otro
editarLa clase de equivalencia de triángulos similares con es generada por[32]
con enteros tales que , donde es el número áureo .
Téngase en cuenta que todos los triángulos con (ya sea con lados enteros o no) satisfacen .
Triángulos enteros con un ángulo tres veces otro
editarSe puede generar la clase de equivalencia completa de triángulos similares que satisfacen B = 3A usando las fórmulas[34]
donde y son enteros tales que .
Téngase en cuenta que todos los triángulos con B = 3A (ya sea con lados enteros o no) satisfacen .
Triángulos enteros con tres ángulos racionales
editarEl único triángulo entero con tres ángulos racionales (números racionales de grados, o fracciones equivalentes racionales de un giro completo) es el triángulo equilátero.[3] Esto se debe a que los lados enteros implican tres cosenos racionales por el teorema del coseno, y por el teorema de Niven un coseno racional coincide con un ángulo racional si y solo si el coseno es igual a 0, ± 1/2 o ± 1. Los únicos que dan un ángulo estrictamente entre 0° y 180° son el valor del coseno 1/2 con el ángulo de 60°, el valor del coseno -1/2 con el ángulo de 120° y el valor del coseno 0 con el ángulo de 90°. La única combinación de tres de estos, permitiendo el uso múltiple de cualquiera de ellos y sumando 180°, es de tres ángulos de 60°.
Triángulos enteros con una relación entera entre circunradio e inradio
editarLas condiciones se conocen en términos de curva elíptica para que un triángulo entero tenga una relación entera N del cociente entre el circunradio y el inradio.[35][36] El caso más pequeño, el del triángulo equilátero, tiene N = 2. En todos los casos conocidos, N ≡ 2 (mod 8), es decir, N-2 es divisible por 8.
Pares de triángulos 5-Con
editarUn par de triángulos 5-Con son semejantes pero no congruentes, y se caracterizan por compartir tres ángulos y dos longitudes de lado. Un par de triángulos 5-Con enteros primitivos, en los que los cuatro lados enteros distintos (dos lados que aparecen en ambos triángulos y otro lado en cada triángulo) no comparten ningún factor primo, tienen tripletes de lados
- y
para enteros coprimos positivos x e y. El ejemplo más pequeño es el par (8, 12, 18), (12, 18, 27), generado por x = 2, y = 3.
. Triángulos enteros particulares
editar- El único triángulo con enteros consecutivos para lados y área tiene lados (3, 4, 5) y área 6.
- El único triángulo con enteros consecutivos para una altura y los lados tiene lados (13, 14, 15) y la altura del lado de 14 igual a 12.
- El triángulo (2, 3, 4) y sus múltiplos son los únicos triángulos con lados enteros en la progresión aritmética y que tienen la propiedad del ángulo exterior complementario.[37][38][39] Esta propiedad establece que si el ángulo C es obtuso y si un segmento es lanzado desde B perpendicularmente a AC extendido hasta P, entonces ∠CAB = 2∠CBP.
- El triángulo (3, 4, 5) y sus múltiplos son los únicos triángulos rectángulos enteros que tienen lados en progresión aritmética.[39]
- El triángulo (4, 5, 6) y sus múltiplos son los únicos triángulos con un ángulo que es el doble de otro y que tiene lados enteros en la progresión aritmética.[39]
- El triángulo (3, 5, 7) y sus múltiplos son los únicos triángulos con un ángulo de 120° y que tienen lados enteros en progresión aritmética.[39]
- El único triángulo entero con área = semiperímetro[40] tiene lados (3, 4, 5).
- Los únicos triángulos enteros con área = perímetro tienen lados[40][41] (5, 12, 13), (6, 8, 10), (6, 25, 29), (7, 15, 20) y (9, 10, 17). De estos, los primeros dos, pero no los tres últimos, son triángulos rectángulos.
- Existen triángulos enteros con tres medianas[9]: p. 64 racionales. Los lados más pequeños tienen (68, 85, 87). Otros incluyen (127, 131, 158), (113, 243, 290), (145, 207, 328) y (327, 386, 409).
- No hay triángulos pitagóricos isósceles.[15]
- Los únicos triángulos pitagóricos primitivos para los cuales el cuadrado del perímetro es igual a un múltiplo entero del área son (3, 4, 5) con el perímetro 12 y el área 6 y con la relación entre el perímetro al cuadrado y el área de 24; (5, 12, 13) con el perímetro 30 y el área 30 y con la proporción del perímetro al cuadrado respecto al área de 30; y (9, 40, 41) con el perímetro 90 y el área 180 y con la relación del perímetro al cuadrado y el área de 45.[42]
Véase también
editar- Pentágono de Robbins, un pentágono cíclico con lados enteros y área entera
- Ladrillo de Euler, un cuboide con bordes enteros y diagonales de caras enteras
- Tetraedro
Referencias
editar- ↑ Carmichael, R. D. (1959) [1914]. «Diophantine Analysis». En R. D. Carmichael, ed. The Theory of Numbers and Diophantine Analysis. Dover. pp. 11–13.
- ↑ Somos, M., "Rational triangles", http://somos.crg4.com/rattri.html Archivado el 4 de junio de 2018 en Wayback Machine.
- ↑ a b Conway, J. H., and Guy, R. K., "The only rational triangle", in The Book of Numbers, 1996, Springer-Verlag, pp. 201 and 228–239.
- ↑ a b Tom Jenkyns and Eric Muller, Triangular Triples from Ceilings to Floors, American Mathematical Monthly 107:7 (August 2000) 634–639
- ↑ Ross Honsberger, Mathematical Gems III, pp. 39–37
- ↑ a b Zelator, K., "Triangle Angles and Sides in Progression and the diophantine equation x2+3y2=z2", Cornell Univ. archive, 2008
- ↑ Jahnel, Jörg (2010). When is the (Co)Sine of a Rational Angle equal to a rational number?. arXiv:1006.2938.
- ↑ Carmichael, R. D. The Theory of Numbers and Diophantine Analysis. New York: Dover, 1952.
- ↑ a b Sierpiński, Wacław. Pythagorean Triangles, Dover Publ., 2003 (orig. 1962).
- ↑ (sucesión A009111 en OEIS) List of ordered areas of Pythagorean triangles (consultado el 2017-03-03)
- ↑ a b Richinick, Jennifer, "The upside-down Pythagorean Theorem", Mathematical Gazette 92, July 2008, 313–317.
- ↑ Voles, Roger, "Integer solutions of a−2+b−2=d−2", Mathematical Gazette 83, July 1999, 269–271.
- ↑ Buchholz, R. H.; MacDougall, J. A. (1999). «Heron Quadrilaterals with sides in Arithmetic or Geometric progression». Bulletin of the Australian Mathematical Society 59: 263-269.
- ↑ Mitchell, Douglas W., "Heron triangles with ∠B=2∠A", Mathematical Gazette 91, July 2007, 326–328.
- ↑ a b Sastry, K. R. S., "Construction of Brahmagupta n-gons", Forum Geometricorum 5 (2005): 119–126.
- ↑ Yiu, P., "CRUX, Problem 2331, Proposed by Paul Yiu" Archivado el 5 de septiembre de 2015 en Wayback Machine., Memorial University of Newfoundland (1998): 175-177
- ↑ Yui, P. and Taylor, J. S., "CRUX, Problem 2331, Solution" Archivado el 16 de febrero de 2017 en Wayback Machine. Memorial University of Newfoundland (1999): 185-186
- ↑ a b Li Zhou, “Primitive Heronian Triangles With Integer Inradius and Exradii”, Forum Geometricorum 18, 2018, pp. 71–77.
- ↑ Wacław Sierpiński, Pythagorean Triangles, Dover Publications, 2003 (orig. ed. 1962).
- ↑ Parry, C. F. (1991). «Steiner–Lehmus and the automedian triangle». The Mathematical Gazette 75 (472): 151-154. JSTOR 3620241..
- ↑ Buchholz, R. H.; MacDougall, J. A. (2001). Cyclic Polygons with Rational Sides and Area. CiteSeerX Penn State University. p. 3. «10.1.1.169.6336».
- ↑ P. Yiu, "Heronian triangles are lattice triangles", American Mathematical Monthly 108 (2001), 261–263.
- ↑ Marshall, Susan H.; Perlis, Alexander R. (2012). Heronian tetrahedra are lattice tetrahedra. University of Arizona. p. 2.
- ↑ Zelator, Konstantine, Mathematical Spectrum 39(3), 2006/2007, 59−62.
- ↑ a b c De Bruyn,Bart, "On a Problem Regarding the n-Sectors of a Triangle", Forum Geometricorum 5, 2005: pp. 47–52.
- ↑ Sastry, K. R. S., "Integer-sided triangles containing a given rational cosine", Mathematical Gazette 68, December 1984, 289−290.
- ↑ Gilder, J., Integer-sided triangles with an angle of 60°", Mathematical Gazette 66, December 1982, 261 266
- ↑ a b Burn, Bob, "Triangles with a 60° angle and sides of integer length", Mathematical Gazette 87, March 2003, 148–153.
- ↑ a b Read, Emrys, "On integer-sided triangles containing angles of 120° or 60°", Mathematical Gazette 90, July 2006, 299−305.
- ↑ Selkirk, K., "Integer-sided triangles with an angle of 120°", Mathematical Gazette 67, December 1983, 251–255.
- ↑ Hirschhorn, Michael D., "Commensurable triangles", Mathematical Gazette 95, March 2011, pp. 61−63.
- ↑ a b Deshpande,M. N., "Some new triples of integers and associated triangles", Mathematical Gazette 86, November 2002, 464–466.
- ↑ Willson, William Wynne, "A generalisation of the property of the 4, 5, 6 triangle", Mathematical Gazette 60, June 1976, 130–131.
- ↑ Parris, Richard (November 2007). College Mathematics Journal 38 (5): 345-355.
- ↑ MacLeod, Allan J., "Integer triangles with R/r = N", Forum Geometricorum 10, 2010: pp. 149−155.
- ↑ Goehl, John F. Jr., "More integer triangles with R/r = N", Forum Geometricorum 12, 2012: pp. 27−28
- ↑ Barnard, T., and Silvester, J., "Circle theorems and a property of the (2,3,4) triangle", Mathematical Gazette 85, July 2001, 312−316.
- ↑ Lord, N., "A striking property of the (2,3,4) triangle", Mathematical Gazette 82, March 1998, 93−94.
- ↑ a b c d Mitchell, Douglas W., "The 2:3:4, 3:4:5, 4:5:6, and 3:5:7 triangles", Mathematical Gazette 92, July 2008.
- ↑ a b MacHale, D., "That 3,4,5 triangle again", Mathematical Gazette 73, March 1989, 14−16.
- ↑ L. E. Dickson, History of the Theory of Numbers, vol.2, 181.
- ↑ Goehl, John F. Jr., "Pythagorean triangles with square of perimeter equal to an integer multiple of area", Forum Geometricorum 9 (2009): 281–282.