Distribución binomial
En teoría de la probabilidad y estadística, la distribución binomial o distribución binómica es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de ensayos de Bernoulli independientes entre sí con una probabilidad fija de ocurrencia de éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, solo dos resultados son posibles, a uno de estos se le denomina “éxito” y tiene una probabilidad de ocurrencia y al otro se le denomina “fracaso” y tiene una probabilidad .[2]
| Distribución binomial | ||
|---|---|---|
|
Función de masa de probabilidad Función de probabilidad | ||
|
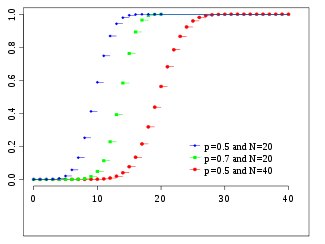
Función de distribución acumulada Función de distribución de probabilidad | ||
| Parámetros |
número de ensayos (entero) probabilidad de éxito (real) | |
| Dominio | ||
| Función de probabilidad (fp) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | Uno de [1] | |
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | ||
| Entropía | ||
| Función generadora de momentos (mgf) | ||
| Función característica | ||
La distribución binomial se utiliza con frecuencia para modelizar el número de aciertos en una muestra de tamaño n extraída con reemplazo de una población de tamaño N. Si el muestreo se realiza sin reemplazo, las extracciones no son independientes, por lo que la distribución resultante es una distribución hipergeométrica, no una distribución binomial. Sin embargo, para N mucho mayores que n, la distribución binomial sigue siendo una buena aproximación, y se utiliza ampliamente.
Más matemáticamente, la distribución binomial es una distribución discreta de probabilidad descrita por dos parámetros: n el número de experimentos realizados, y p la probabilidad de éxito. Para cada experimento llamado ensayo Bernoulli, utilizamos una variable aleatoria que toma el valor 1 cuando se consigue un éxito y el valor 0 en caso contrario. La variable aleatoria, suma de todas estas variables aleatorias, cuenta el número de éxitos y sigue una distribución binomial. Es posible entonces obtener la probabilidad de k éxitos en una repetición de n experimentos:
En esta fórmula interviene el coeficiente binomial del que se deriva el nombre de la ley.
La importancia de esta ley es en primer lugar histórica ya que fue objeto de estudio del Teorema de De Moivre-Laplace, resultado del xviii fundador de la teoremas de convergencia. Una distribución binomial también se puede utilizar para modelar situaciones simples de acertar o fallar, un juego de lanzar una moneda, por ejemplo. El cálculo de su función de probabilidad se vuelve rápidamente tedioso cuando n} es grande, es posible entonces utilizar aproximaciones por otras leyes de probabilidad|leyes de probabilidad como la distribución de Poisson o la distribución normal y utilizar tablas de valores.
La ley binomial se utiliza en diversos campos de estudio, especialmente a través de pruebas estadísticas que permiten interpretar datos y tomar decisiones en situaciones que dependen del azar. Debido a su sencilla definición, es una de las leyes de probabilidad que se estudian en los cursos introductorios de teoría de la probabilidad.
Explicación intuitiva editar
Primeros ejemplos editar
Cara o cruz editar
Consideremos n lanzamientos sucesivos de una moneda. Entonces el número de veces que la moneda aparece en la cara de la cruz sigue la distribución binomial donde el número de experimentos realizados es n y la probabilidad de éxito es
Lanzar un dado editar
Consideremos n lanzamientos sucesivos de un dado de 6 caras. Entonces el número de veces que sale un 1 sigue la distribución binomial donde el número de experimentos realizados es n y la probabilidad de éxito es .
Definición intuitiva editar
Una ley de Bernoulli describe el comportamiento de un experimento aleatorio que tiene dos posibles resultados tradicionalmente llamados éxito y fracaso[3]. Un experimento de este tipo se denomina ensayo de Bernoulli. Por ejemplo, en un lanzamiento de cara o cruz, cara puede considerarse un éxito y cruz un fracaso. En este modelo, la probabilidad de éxito es un valor fijo, es decir, permanece constante en cada renovación del experimento aleatorio. Esta probabilidad de éxito se denomina "p".
Consideremos la situación en la que un experimento aleatorio de este tipo (dos resultados posibles y una probabilidad fija) se repite un cierto número de veces de forma independiente; denotemos n este número de veces. Esta repetición independiente de ensayos de Bernoulli se denomina Esquema de Bernoulli o simplemente Ensayos de Bernoulli[4]. Una distribución binomial describe el número de veces que aparece el éxito en los n experimentos realizados. Dado que el número de éxitos obtenidos es un valor aleatorio, una distribución binomial se describe dando las probabilidades de que el éxito se produzca precisamente k veces en los n ensayos.
Árbol de probabilidades editar
Una forma visual de representar una secuencia de experimentos es utilizar un árbol de probabilidad. Cada suceso está representado por dos ramas: una para el éxito y otra para el fracaso. En cada extremo, se añaden dos ramas (éxito y fracaso) para el siguiente ensayo. Esto se repite hasta que se alcanza el número total de sucesos. En cada extremo final, se puede contar el número de éxitos. Se multiplica el número de veces que k tiene éxito por la probabilidad de que k tenga éxito para obtener la probabilidad correspondiente de la distribución binomial.
Definición editar
Notación editar
Si una variable aleatoria discreta tiene una distribución binomial con parámetros y con entonces escribiremos .
Función de Probabilidad editar
Si entonces su función de probabilidad está dada por
para , siendo
el coeficiente binomial y se lee “las combinaciones de en “.
En ocasiones, para calcular las probabilidades binomiales se utiliza la siguiente fórmula recursiva para calcular en términos de
Función de Distribución Acumulada editar
La función de distribución acumulada de una variable aleatoria está dada por
También puede ser expresada en términos de la función beta incompleta como
que es equivalente a la función de distribución acumulada de la distribución F.
La distribución binomial es la base del test binomial de significación estadística.
Experimento binomial editar
Existen muchas situaciones en las que se presenta una experiencia binomial. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). El valor de ambas posibilidades ha de ser constante en todos los experimentos, y se denotan como y respectivamente o como y de forma alternativa.
Se designa por a la variable que mide el número de éxitos que se han producido en los experimentos.
Cuando se dan estas circunstancias, se dice que la variable sigue una distribución de probabilidad binomial.
Ejemplo editar
Supongamos que se lanza 51 veces un dado de 6 caras y queremos calcular la probabilidad de que el número 3 salga 20 veces.
En este problema un ensayo consiste en lanzar el dado una vez. Consideramos un éxito si obtenemos un 3 pero si no sale 3 lo consideramos como un fracaso. Defínase como el número de veces que se obtiene un 3 en 51 lanzamientos.
En este caso tenemos por lo que la probabilidad buscada es
Propiedades editar
Si es una variable aleatoria discreta tal que entonces
La primera de ellas es fácil de demostrar, por definición de Esperanza
el primer término de la suma, es decir, para el término vale cero por lo que podemos iniciar la suma en
Dado que
para .
Reemplazando lo anterior en la expresión de obtenemos
Haciendo el cambio de índice obtenemos
Finalmente por la fórmula de Newton (Teorema del binomio)
Obtenemos
- .
Distribuciones Relacionadas editar
Suma de Binomiales editar
Si y son variables aleatorias independientes con la misma probabilidad entonces la variable aleatoria también es una variable aleatoria con distribución binomial con parámetros y , es decir
Distribución Bernoulli editar
Si son variables aleatorias independientes e idénticamente distribuidas tales que entonces
Lo anterior es equivalente a decir que la distribución Bernoulli es un caso particular de la distribución Binomial cuando , es decir, si entonces .
Distribuciones limitantes editar
Teorema límite de Poisson editar
Si y es tal que el producto entre ambos parámetros tiende a , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro .
Teorema de De Moivre-Laplace editar
Si es una variable aleatoria con media y varianza entonces
conforme , esta aproximación es buena si y .
Propiedades reproductivas editar
Si son variables aleatorias independientes tales que con entonces
Inferencia estadística editar
Estimación de parámetros editar
Cuando se conoce n, el parámetro p puede estimarse utilizando la proporción de aciertos:
Este estimador se encuentra utilizando estimador de máxima verosimilitud y también el método de los momentos. Este estimador es insesgado y uniforme con mínima varianza, demostrado mediante el Teorema de Lehmann–Scheffé, ya que se basa en un estadístico mínimo suficiente y completo (es decir: x). También es consistente tanto en probabilidad como en MSE.
También existe un estimador de Bayes de forma cerrada para p cuando se utiliza la distribución Beta como conjugada de la probabilidad a priori. Cuando se utiliza un a priori, el estimador medio posterior es:
El estimador de Bayes es asintóticamente eficiente y a medida que el tamaño de la muestra se aproxima a infinito (n → ∞), se aproxima a la solución de máxima verosimilitud. El estimador de Bayes es sesgado, cuánto depende de los priores, admisible y consistente en probabilidad.
Para el caso especial de utilizar la distribución uniforme estándar como a priori no informativo, , el estimador de la media a posteriori se convierte en:
Este método se denomina regla de sucesión, que fue introducido en el siglo XVIII por Pierre-Simon Laplace.
Cuando se estima p con sucesos muy raros y un n pequeño (por ejemplo: si x=0), entonces utilizar el estimador estándar conduce a lo que a veces es poco realista y poco deseable. En estos casos existen varios estimadores alternativos.[5] Una forma es utilizar el estimador de Bayes, lo que lleva a:
Otro método consiste en utilizar el límite superior del intervalo de confianza obtenido mediante la regla de tres:
Intervalos de confianza editar
Incluso para valores bastante grandes de n, la distribución real de la media es significativamente no normal.[6] Debido a este problema se han propuesto varios métodos para estimar intervalos de confianza.
En las ecuaciones para intervalos de confianza que se presentan a continuación, las variables tienen el siguiente significado:
- n 1 es el número de aciertos de n, el número total de ensayos.
- es la proporción de aciertos
- es el cuantil de una distribución normal estándar (es decir, probit) correspondiente a la tasa de error objetivo . Por ejemplo, para un nivel de confianza del 95% el error = 0,05, por lo que = 0,975 y = 1,96.
Véase también editar
Referencias editar
- ↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.
- ↑ Wadsworth, G. P. (1960). Introduction to Probability and Random Variables. New York: McGraw-Hill. p. 52.
- ↑ Gossett, 2009, p. 310.
- ↑ Dodge, 2007, p. 175.
- ↑ Razzaghi, Mehdi (2002). «Sobre la estimación de la probabilidad de éxito binomial con ocurrencia cero en la muestra». Journal of Modern Applied Statistical Methods 1 (2): 326-332. doi:10.22237/jmasm/1036110000.
- ↑ Brown, Lawrence D.; Cai, T. Tony; DasGupta, Anirban (2001), html «Estimación de intervalos para una proporción binomial», Statistical Science 16 (2): 101-133, doi:10.1214/ss/1009213286, consultado el 5 de enero de 2015 Parámetro desconocido
|citeseerx=ignorado (ayuda).
Bibliografía editar
- Hirsch, Werner Z. (1957). «Binomial Distribution—Success or Failure, How Likely Are They?». Introduction to Modern Statistics. New York: MacMillan. pp. 140-153.
- Neter, John; Wasserman, William; Whitmore, G. A. (1988). Applied Statistics (Third edición). Boston: Allyn & Bacon. pp. 185–192. ISBN 0-205-10328-6.
- Patrick Bogaert (2005). Probabilités pour scientifiques et ingénieurs. De Boeck Supérieur. p. 402. ISBN 2-8041-4794-0.
Enlaces externos editar
- Wikimedia Commons alberga una categoría multimedia sobre Distribución binomial.
- Tablas de la distribución binomial, hasta n=20, en formato PDF.
- Calculadora Distribución binomial
- Cálculo de la probabilidad de una distribución binomial con R (lenguaje de programación)
- Generación estadística de la distribución binomial con números aleatorios usando Python (lenguaje de programación)
- Interactive graphic: Univariate Distribution Relationships
- Binomial distribution formula calculator
- Difference of two binomial variables: X-Y or |X-Y|
- Querying the binomial probability distribution in WolframAlpha