Vector
En matemática, un vector fijo es un segmento de recta orientado en el espacio euclídeo. La longitud de dicho segmento se denomina módulo del vector, que es siempre un número no negativo. La recta que lo contiene se denomina recta soporte. Cualquiera de las rectas paralelas a esta, o bien sus semirrectas que apuntan en el mismo sentido dado por la orientación del vector, determinan la dirección del vector.[a] Para muchas aplicaciones el punto inicial es irrelevante, por lo que no se hace distinción entre dos vectores que tienen el mismo módulo y dirección; se consideran equivalentes aunque su punto inicial sea diferente.[1] La clase de equivalencia de todos los vectores fijos de igual módulo y dirección se denomina vector libre o simplemente vector[2][b].
En física los vectores se emplean para describir las magnitudes vectoriales, a diferencia de las magnitudes escalares, que se pueden expresar simplemente con un número. Por ejemplo, para determinar la velocidad de un objeto en movimiento, como un automóvil, no basta con una cantidad en kilómetros o millas por hora (lo que marca el velocímetro, que sería el módulo de la velocidad) sino que es necesario describir también la dirección en la que se produce dicho movimiento. Otros ejemplos de magnitudes vectoriales son la fuerza, el desplazamiento o el campo eléctrico.

Un vector fijo queda completamente determinado por un punto inicial y un punto final ; o alternativamente por el punto inicial, el módulo y la dirección. Dado un sistema de coordenadas del espacio -dimensional (un punto origen y una base de vectores), el vector correspondiente (módulo y dirección) queda unívocamente determinado mediante números, llamados componentes del vector. Estos se obtienen al restar, una por una, cada coordenada del punto final menos la correspondiente del punto inicial (). El conjunto de todos los posibles vectores en el espacio -dimensional se denota como , y se compone de todas las -tuplas de números reales.[3] Estos vectores reales se generalizan de forma natural a los vectores complejos, que son -tuplas de números complejos (y cuyo conjunto se denota ).[4]
Dos vectores se pueden sumar, sumando las componentes correspondientes, para obtener un tercero. El vector resultante es el obtenido al concatenar uno a continuación del otro. Un vector también se puede multiplicar por un escalar (un número ), multiplicando cada componente por dicho número. El vector que se obtiene de esta operación tiene la misma dirección, pero su módulo resulta multiplicado por , es decir, se escala por un factor . Juntando ambas operaciones se obtienen combinaciones lineales de vectores.[5]
En álgebra abstracta se define el concepto más general de espacio vectorial sobre un cuerpo : un conjunto dotado de dos operaciones que se comportan como la suma de vectores y el producto por escalares (elementos de ) de los vectores geométricos. En este contexto, un vector se define como un elemento de un espacio vectorial. Los espacios euclídeos de dimensión finita, como el plano o el espacio tridimensional , son casos particulares de este tipo de estructura matemática en lo que se refiere al álgebra (sus dos operaciones).[6] No obstante, la generalización de otras características geométricas de los vectores, como el módulo o el ángulo entre vectores requieren de otras estructuras adicionales (norma, producto escalar...) que no todos los espacios vectoriales poseen.[7]
Conceptos fundamentales en vectores euclídeos
editarEsta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, los componentes de un vector euclídeo o geométrico, así como la notación de los mismos, etc. En otra sección más adelante se tratan otro tipo de vectores más generales.
Definición
editarExisten dos formas de definir el concepto de vector: hay una definición analítica, por medio de componentes,[8] y una definición geométrica, por medio de segmentos orientados.[9] Ambas definiciones son equivalentes, y la conexión entre ambas viene dada por la geometría analítica, que describe puntos del espacio mediante coordenadas.
Un vector (real) de dimensión es una -tupla de números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión se representa como (formado mediante el producto cartesiano de veces el conjunto de números reales). Así, un vector perteneciente al espacio se representa como:
, donde para todo .
En geometría. un vector fijo del espacio euclidiano es un segmento orientado, definido por un punto inicial u origen y un punto final o extremo. En un vector fijo se pueden distinguir los siguientes elementos geométricos:
| El punto de aplicación es el punto inicial del segmento orientado. | |
| El módulo es la longitud del segmento expresado mediante un número no negativo. Cuando el vector representa una magnitud física, dicha cantidad estará expresada en alguna unidad de medida. | |
| La recta soporte o línea de acción es la recta contiene al segmento. El conjunto de todas las rectas paralelas a esta se denomina dirección. | |
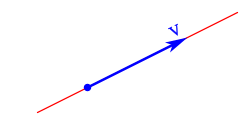
| El sentido, indicado por la orientación (del punto inicial hacia el punto final), siendo uno de los dos posibles sobre la recta soporte. Se representa gráficamente con una flecha. |
Dos vectores fijos se consideran equipolentes si tienen igual módulo, dirección y sentido. La relación entre vectores fijos dada por «ser equipolente» es una relación de equivalencia, y la clase de todos los vectores equipolentes a uno dado se denomina vector (o vector libre). En cierto modo, un vector se puede desplazar libremente y fijarse a cualquier punto del espacio, pero sin desviarlo, invertirlo o escalarlo. Esto es porque se puede tomar cualquiera los vectores fijos de la clase de equivalencia como representante del vector libre.
En física, a veces es preciso considerar el punto de aplicación de la magnitud vectorial considerada, o al menos su recta de acción. En este último caso, la magnitud se describe mediante un vector deslizante: la clase de todos los vectores fijos que comparten igual módulo, recta de aplicación y sentido. En cierto sentido, es como si se pudiera deslizar el vector a lo largo de la recta de acción, pero sin invertirlo o escalarlo.
Clasificación de vectores
editarSegún los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse:
- Vectores fijos o ligados: tienen un determinado punto de aplicación.
- Vectores libres: pueden estar aplicados en cualquier punto del espacio.
- Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
Podemos referirnos también a:
- Vectores unitarios: vectores de módulo uno.
- el vector nulo: es un vector de módulo igual a cero.
En función de las características de un vector respecto de otro, dos vectores pueden ser:
- Vectores paralelos: si los dos vectores tienen igual dirección.
- Vectores opuestos: si los dos vectores tienen igual magnitud y dirección, pero son de sentidos contrarios.[10]. Los vectores opuestos son paralelos.
- Vectores perpendiculares: si las direcciones de los dos vectores forman un ángulo recto, lo cual sucede precisamente cuando su producto escalar es cero.
En función de sus respectivas rectas de acción, dos vectores pueden ser:
- Vectores concurrentes o angulares: sus líneas de acción pasan por un mismo punto.
- Vectores colineales: sus recta de acción coinciden. Los vectores colineales son un caso particular de los vectores paralelos.
- Vectores coplanarios: vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).
Dirección vs dirección y sentido
editarEn inglés, la palabra direction indica tanto la dirección (orientation) como el sentido (sense), con lo que para definir un vector basta con especificar el módulo y la dirección (magnitude and direction).[11]
No obstante, en lengua española, un vector se distingue por tres características: módulo, dirección y sentido.[10][12][13]
Notación
editarEn el espacio, un segmento orientado (un vector fijo) se denota con dos letras mayúsculas y una flecha hacia la derecha encima, que indican su origen y extremo respectivamente. Por ejemplo, un vector fijo con punto inicial en y punto final en , se representa como . Esta notación se utiliza frecuentemente en física para denotar los vectores que representan el desplazamiento.
En general, los vectores (libres) se representan mediante letras minúsculas. En los textos manuscritos, para diferenciarlos de los escalares, los vectores se representan mediante una flecha (o alternativamente con un trazo) sobre la letra que designa el vector, como por ejemplo (o bien ). En los textos impresos, es frecuente representar los vectores mediante letras en negrita (como ).
Como excepción, los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un acento circunflejo, por ejemplo .
El módulo de un vector se representa encerrando mediante dos barras verticales la letra que designa dicho vector. Así, el módulo de se representa como (en textos impresos, ).
En álgebra abstracta, se definen espacios vectoriales sin una clara interpretación geométrica (espacios de matrices, de polinomios, de funciones,...). En estos casos se emplean otras notaciones, apropiadas para cada caso. En algunos de estos espacios, en los llamados espacios normados, se define la norma de un vector (que generaliza la idea del módulo) que se suele representar con doble barra vertical: la norma de se representa como .
Componentes de un vector
editarUn vector en el espacio euclidiano tridimensional se puede expresar como una combinación lineal de tres vectores unitarios o versores, que son perpendiculares entre sí y constituyen una base vectorial.
En coordenadas cartesianas, los vectores unitarios se representan por , , , ( o u, v, w) paralelos a los ejes , , correspondientes. Los componentes del vector en una base predeterminada pueden escribirse entre paréntesis y separadas con comas:
o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será
Estas representaciones son equivalentes entre sí, y los valores , , , son los componentes de un vector que, salvo que se indique lo contrario, son números reales.
Una representación conveniente de las magnitudes vectoriales es mediante un vector columna o un vector fila, particularmente cuando están implicadas operaciones matrices (tales como el cambio de base), del modo siguiente:
Por ejemplo, los vectores unitarios se expresarían de la siguiente manera:
El lema de Zorn, consecuencia del axioma de elección, permite establecer que todo espacio vectorial admite una base vectorial, por lo que todo vector es representable como el producto de unos componentes respecto a dicha base. Dado un vector, solamente existen un número finito de componentes diferentes de cero.
Operaciones con vectores
editarCon los vectores, siempre que pertenezcan a un mismo espacio, se pueden realizar diversas operaciones. La principal operación entre vectores es la suma, en la que se toman dos vectores para obtener un tercero. La otra operación fundamental es el «producto por un escalar» en el que se multiplica un vector por un factor de escala para obtener otro vector. Otras operaciones posibles son el producto escalar, el producto vectorial y el producto mixto, aunque las dos últimas no están definidas en todas las dimensiones.
En general, las operaciones se definen sobre los vectores (libres). Existen reglas para obtener gráficamente los resultados de estas operaciones. Para ello, primeramente se deben elegir representantes (vectores fijos equivalentes a cada uno de los operandos), estableciendo un punto inicial para cada uno de ellos. Cuando el resultado sea un vector, este será el vector libre asociado al vector fijo así obtenido. También hay reglas algebraicas para operar con los vectores a partir de sus componentes respecto de cierta base, que tiene que ser la misma para todos los operandos y para el resultado.
Suma de vectores
editarConstrucción geométrica
editarLa suma de dos vectores da como resultado un tercer vector. Para obtener éste, se escogen dos vectores fijos concatenados como representantes de los dos sumandos: tales que el extremo final del primero coincida con el extremo inicial del segundo. El vector suma se corresponde con el vector fijo que tiene por punto inicial el inicial del primer vector y por punto final el final del segundo. Si se invierte el orden de los sumandos, la suma no cambia, como se puede ver al completar el paralelogramo cuyos lados están dados por los vectores que se suman. Es decir, la suma de vectores satisface la propiedad conmutativa.[1]
Se puede generalizar esta operación a la suma de un número de vectores. Para obtener la suma total, se concatenan todos ellos uno a continuación del otro. El vector resultante es el que une el punto inicial del primero con el punto final del último. Las sumas parciales que hay que realizar pueden hacerse en cualquier orden, dado que los puntos inicial y final no cambian, por lo que la suma de vectores también satisface la propiedad asociativa.
Expresión algebraica de la suma por componentes
editarConocidas las componentes de dos vectores, respecto de la misma base, por ejemplo
el vector suma de v y w es el que tiene componentes, respecto de la misma base
Es decir, la suma se obtiene sumando componente por componente. La suma vectorial es una generalización de la suma de números reales y como tal comparte muchas de sus propiedades: la propiedad conmutativa y la propiedad asociativa son inmediatas. También existe un elemento neutro para la suma de vectores: el vector nulo. Este vector nulo tiene todas sus componentes iguales a 0, y por tanto sumarlo a cualquier otro vector no tiene ningún efecto: para todo vector v se tiene que v+0 = v. Al igual que para la suma usual, todo vector tiene también su elemento opuesto: dado un vector v de componentes existe un vector -v con componentes y tal que v+(-v)=0.[14] Todas estas propiedades implican que los vectores de un mismo espacio forman un grupo respecto de la suma.
Suma de magnitudes vectoriales
editarEn física, la suma de dos vectores tiene sentido solo en ciertos contextos. Ambos vectores tienen que representar la misma magnitud vectorial. Por ejemplo, carece de sentido sumar fuerzas con velocidades. Además, la suma tiene que tener un sentido físico, como por ejemplo sumar las distintas fuerzas aplicadas sobre una masa puntual para obtener la resultante de fuerzas. Sustituir las fuerzas individuales por su vector suma, aplicado en la misma masa puntual, es un sistema físico equivalente.
En un sólido rígido (con extensión) distintas fuerzas pueden actuar en puntos distintos. Aún así se pueden sumar, desplazandolos, siempre y cuando se mantenga su recta de acción. Si existe un punto común entre las varias rectas, se pueden deslizar los vectores hasta dicho punto y sumarlos, siendo la recta de acción de la resultante la que pasa por dicho punto. Si no hay un punto común, el sistema equivalente estará formado por una fuerza (la suma de los vectores libres de las fuerzas individuales) y por un momento de fuerza. En este caso, se deberá optar por un punto de aplicación para la fuerza resultante: el sistema equivalente está formado por este vector suma aplicado en tal punto y un momento de fuerza, igual a la suma de los momentos de cada una de las fuerzas actuantes, calculados respecto del punto de aplicación elegido.
Producto de un vector por un escalar
editarEl producto por un escalar, también llamado multiplicación escalar, es una operación entre un vector y un escalar. El resultado es otro vector de igual dirección (pero orientado en sentido contrario si el escalar es negativo) y cuyo módulo resulta multiplicado por el valor absoluto del escalar.
Si se conocen las componentes de un vector respecto de una base cualquiera, el producto de v por un escalar tiene por componentes, en la misma base
es decir, se multiplica cada componente de v por .
El producto de un vector por un escalar satisface las siguientes propiedades. Dados escalares , y vectores y cualesquiera, se verifican:
- la propiedad distributiva respecto de la suma de escalares
- y respecto de la suma de vectores
- La multiplicación por la unidad no tiene ningún efecto:
Combinaciones lineales
editarUtilizando las dos operaciones anteriores, se puede plantear una expresión de la forma
llamada combinación lineal de los vectores .[15] Los escalares se denominan coeficientes.
Un vector se puede expresar como una combinación lineal de los vectores de una base. Si un vector v tiene por componentes respecto de la base entonces
De hecho, los coeficientes son los únicos escalares que hacen que la igualdad anterior sea cierta, es decir, las componentes de un vector respecto de una base son únicas.[16]
Las combinaciones lineales admiten las mismas dos operaciones que los vectores (suma y multiplicación escalar) según las reglas usuales del álgebra. Ello es especialmente útil cuando se expresan los vectores como combinaciones lineales de los vectores de la base. En tres dimensiones es habitual utilizar la base canónica denotada como . Sean por ejemplo los vectores
Entonces, se puede simplificar una combinación lineal como por ejemplo
Esta forma de operar con combinaciones lineales es compatible con las expresiones algebraicas dadas más arriba para la suma y la multiplicación escalar, es decir:
Producto escalar
editarEl producto escalar de dos vectores tiene como resultado un número (un escalar), que equivale al producto de los módulos de los vectores por el coseno del ángulo entre ellos. Cuando ambos vectores son perpendiculares, el ángulo entre ellos es recto y por tanto el coseno se anula, con lo que su producto escalar es cero. El producto escalar de un vector consigo mismo es el cuadrado de su módulo.[17]
Cuando las componentes de los dos vectores están expresadas respecto de una base ortonormal, el producto escalar se puede obtener como el producto de la matriz fila del primer vector por la matriz columna del segundo:[18]
En cambio, cuando la base no es ortonormal el producto escalar de y es igual al producto de tres matrices , donde es la matriz de Gram. Las entradas de esta matriz son los productos escalares de los vectores de la base entre sí. De ahí que cuando la base es ortonormal, la matriz de Gram es la matriz identidad.
Producto vectorial
editarEn el espacio tridimensional, el producto vectorial de dos vectores da como resultado otro vector perpendicular a los anteriores. Su módulo equivale al producto de los módulos de los vectores por el seno del ángulo entre ellos. Su sentido se obtiene mediante la regla de la mano derecha. Cuando ambos vectores son paralelos, el seno se anula, con lo que su producto vectorial es el vector nulo. Respecto de una base ortonormal , el producto escalar de los vectores y se puede obtener expandiendo el determinante[19]
Es posible generalizar el producto vectorial a espacios con otras dimensiones, aunque son de escaso interés. En cambio, existe una generalización del producto vectorial llamada producto mixto, que permite calcular el volumen de un paralelepípedo a partir de los tres vectores que se obtienen de sus aristas.
Funciones vectoriales
editarEs posible definir funciones que tomen como argumento un vector, que devuelvan un vector, o ambas cosas. En general, dados dos espacios vectoriales reales de dimensiones y respectivamente, se pueden definir funciones , que a cada vector de dimensión le asignan un vector de dimensión . Cuando es la unidad, dichas funciones se denominan formas. Una función vectorial queda completamente determinada por sus funciones componentes . Cada función es una forma que asigna a cada vector de la -ésima componente de su vector imagen . La rama del cálculo que estudia estas funciones es el cálculo vectorial.
Las funciones vectoriales se pueden emplear para representar transformaciones geométricas, campos vectoriales o parametrizaciones. Por ejemplo, la trayectoria de un objeto en el espacio se puede describir mediante una función que a cada instante le asigna una posición en el espacio . Una superficie se puede describir mediante coordenadas curvilineas , y en general las variedades -dimensionales se describen mediante cartas (o mapas) que son funciones vectoriales dependientes de variables.
Transformaciones lineales
editarLas transformaciones lineales u operadores lineales son funciones que toman un vector y devuelven otro, del mismo espacio o de otro distinto, y que preservan las combinaciones lineales: dados escalares , y vectores y cualesquiera, una función f es una transformación lineal si se cumple que:[20]
Dadas dos bases y , para los espacios de partida y de llegada respectivamente, la transformación lineal f queda determinada por una matriz . Las columnas de esta matriz son las imágenes por f de los vectores de la base , expresados mediante sus componentes en la base . El orden de esta matriz será , donde es el número de vectores de y el número de vectores de , dimensiones del espacio de llegada y de partida respectivamente. La imagen del vector v por f se obtiene multiplicando la matriz por el vector columna con las componentes de v en la base .[21] Por ejemplo, la matriz
representa una transformación en el plano (en la base canónica), que rota cada vector un ángulo de 90º en sentido positivo (antihorario). Otros ejemplos de transformaciones lineales son las reflexiones, las proyecciones, las homotecias y las formas lineales.
Cambios de base
editarUn problema habitual es, dadas las componentes de un vector respecto de una base , obtener sus componentes respecto de otra base distinta . La función que transforma unas componentes en otras se denomina cambio de base, y es una transformación lineal. La matriz asociada a esta transformación se denomina matriz de cambio de base o matriz de paso. Aplicando la regla general de las transformaciones lineales, las columnas de la matriz de cambio de base son las componentes en la base de los vectores de . Esta matriz es siempre cuadrada e invertible. La matriz inversa representa el cambio de base inverso, es decir, de a .[22] Las nuevas componentes se obtienen al multuplicar esta matriz por el vector columna con las componentes en la base de partida. Por ejemplo en tres dimensiones, si entonces las componentes de un vector v satisfacen la igualdad matricial
Un caso particular de los cambios de base es cuando ambas son bases ortonormales. Entonces la matriz de paso es una matriz ortogonal (en el caso de vectores complejos, unitaria). Estas transformaciones preservan el producto escalar y por tanto son isometrías del espacio (en esencia, preservan distancias y ángulos). Las matrices ortogonales tienen la propiedad de que su inversa es igual a su transpuesta, por lo que es inmediato obtener el cambio de base inverso.[23]
Diferenciación de vectores
editarDado un vector que es función de una variable independiente , su derivada con respecto de la variable t es el vector que se obtiene derivando cada una de sus componentes por separado:
De las reglas usuales para obtener derivadas de funciones, resulta que la diferenciación es una transformación lineal, es decir: la derivada de una combinación lineal es la combinación lineal de las derivadas:
donde son escalares constantes y son vectores variables.
Por ejemplo, en tres dimensiones y respecto de la base canónica, la función vectorial
representa el vector posición (en función del tiempo t) de una una partícula a lo largo de una trayectoria helicoidal alrededor del eje z de radio unidad, como se ilustra en la figura. Su derivada representa la velocidad, que es tambień un vector variable en el tiempo. En cada instante, su dirección es tangente a la curva en el punto que ocupa la partícula. Si se deriva la expresión para , teniendo en cuenta que los vectores de la base son constantes, se tiene:
En general, la derivada de una función vectorial es una transformación lineal que se describe mediante la matriz jacobiana de , cuyas entradas son las derivadas parciales de las componentes.[24]. El cálculo vectorial se dedica al estudio de las funciones vectoriales diferenciables, así como de la aplicación a estas de otros conceptos del análisis matemático como los límites, la continuidad o la integración.
Derivada covariante de un vector
editarCuando en lugar de emplear una "base fija" en todo el dominio de un vector se usan "bases móviles" como cuando se emplean coordenadas curvilíneas la variación total de un vector dependiente del tiempo depende no solo de la variación de componentes como en el caso de la derivada ordinaria sino también de la variación de la orientación de la base. La variación total se llama derivada covariante:
Cuando se emplea una base fija (coordenadas cartesianas) la derivada covariante coincide con la derivada ordinaria. Por ejemplo cuando se estudia el movimiento de una partícula desde un sistema de referencia no inercial en rotación, las aceleraciones de Coriolis y centrípeta se deben a los factores que contienen y otros factores menos comunes.[cita requerida]
Ángulo entre dos vectores
editarEl ángulo determinado por las direcciones de dos vectores y viene dado por:
Descomposiciones de un vector
editarDado un vector y una dirección de referencia dada por un vector unitario se puede descomponer el primer vector en un componente paralela y otro componente perpendicular a la dirección de referencia:
En física esta descomposición se usa en diferentes contextos como descomponer la aceleración en un componente paralela a la velocidad y otro componente perpendicular a la misma. También el tensión mecánica en un punto sobre un plano puede descomponerse en un componente normal al plano y otra paralela.
También dado un campo vectorial definido sobre un dominio de Lipschitz, acotado, simplemente conexo y de cuadrado integrable admite la llamada descomposición Helmholtz como suma de un campo conservativo y un campo solenoidal:
Vectores en el caso general
editarEn matemáticas, se define la estructura de espacio vectorial y a cada uno de los elementos o puntos de ese espacio se les denomina vector. En muchos casos los vectores no pueden ser representados por módulo dirección y sentido. Por ejemplo, en un espacio vectorial complejo sobre los números complejos la noción de módulo no está automáticamente defindida. Igualmente en un espacio vectorial de dimensión infinita, como es el caso de espacios de Hilbert no existe una representación gráfica de los vectores como segmentos orientados.
Magnitudes vectoriales
editarFrente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.
Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.[25] [26]
Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.[10][12][13]
Requerimientos físicos de las magnitudes vectoriales
editarNo cualquier n-tupla de funciones o números reales constituye un vector físico. Para que una n-tupla represente un vector físico, los valores numéricos de los componentes del mismo medidos por diferentes observadores deben transformarse de acuerdo con ciertas relaciones fijas.
En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamados vectores axiales que realmente representan el dual de Hodge de magnitudes tensoriales antisimétricas. El momento angular, el campo magnético y todas las magnitudes en cuya definición interviene el producto vectorial son en realidad pseudovectores o vectores axiales.
En teoría de la relatividad especial, solamente los vectores tetradimensionales cuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante alguna transformación de Lorentz constituyen magnitudes vectoriales. Así los componentes de dos magnitudes vectoriales medidas por dos observadores y deben relacionarse de acuerdo con la siguiente relación:
Donde son los componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.
Véase también
editarNotas
editar- ↑ En los textos en castellano, es habitual con dirección referirse a una recta (o una familia de rectas paralelas), y con sentido a una de las dos semirrectas (o familias de semirrectas paralelas).«2». Compendio de Física. Editorial San Marcos. 2018. ISBN 978-612-315-362-5.
- ↑ También llamado vector euclidiano o vector geométrico para distinguirlo del concepto más genérico de espacio vectorial o de otras acepciones.[cita requerida]
Referencias
editar- ↑ a b (Shafarevich y Remizov, 2013, p. 79-81)
- ↑ (Marsden y Tromba, 2003, pp. 7)
- ↑ (Strang, 2009, §3.1)
- ↑ (Strang, 2009, §10.1)
- ↑ (Marsden y Tromba, 2003, §1.1)
- ↑ (Meyer, 2000, §4.1)
- ↑ (MacCluer, 2009, p. 2)
- ↑ Por ejemplo, así lo define (Strang, 2009).
- ↑ La definición geométrica se puede encontrar en (Shafarevich y Remizov, 2013), mientras que (Marsden y Tromba, 2003, §1.1) presenta ambas simultáneamente.
- ↑ a b c Enrico Bompiani, Universidad Nacional del Litoral, ed., Geometría Analítica, pp. 14-15, ISBN 9789875084339.
- ↑ Mitiguy, Paul, Chapter 2: Vectors and dyadics (en inglés), p. nota 1 en página 2, archivado desde el original el 20 de noviembre de 2012, consultado el 12 de febrero de 2012.
- ↑ a b Llopis, GÁlvez, Rubio, López (1998), Editorial Tebar, ed., Física: curso teórico-práctico de fundamentos físicos de la ingeniería, p. 26-27,36,70,71,82, ISBN 9788473601870, «(cito algunos ejemplos) [de página 26] [Otras magnitudes] llamadas vectoriales, donde no basta conocer su valor numerico, sino que además es necesario dar también su dirección y sentido. [página 70] […] el cual es un vector que en general tendrá distinta dirección y sentido que r(t). [página 71] […] Consecuencia de la definición es que la dirección de este vector derivada, dr/dt, es tangente a la curva indicatriz, su sentido es el de los valors crecientes del parámetro escalar t, y que su módulo es: […]».
- ↑ a b Manuela Blanco Sánchez, Marcial Carreto Sánchez, José Ma González Clouté (1997), Ediciones de la Torre, ed., Programa de diversificación curricular: ámbito científico-tecnológico: 2o. ciclo de ESO, Proyecto Didáctico Quirón. Ciencias y tecnología 102 (ilustrada edición), pp. 200,202,216, ISBN 9788479601867.
- ↑ (Marsden y Tromba, 2003, pp. 3-6)
- ↑ (Meyer, 2000, p. 91)
- ↑ (Strang, 2009, p. 172)
- ↑ Strang, 2009, p. 12.
- ↑ Strang, 2009, p. 11.
- ↑ Marsden y Tromba, 2003, pp. 43-46.
- ↑ (Meyer, 2000, §3.3)
- ↑ (Shafarevich y Remizov, 2013, p. 105)
- ↑ (Shafarevich y Remizov, 2013, §3.4)
- ↑ (Meyer, 2000, §5.6)
- ↑ (Marsden y Tromba, 2003, pp. 133-135)
- ↑ «Euclidean vector» (en inglés). PlanetMath.org. Archivado desde el original el 6 de marzo de 2016. Consultado el 3 de junio de 2010.
- ↑ «Vector» (en inglés). Math Academy Online. Archivado desde el original el 28 de octubre de 2012. Consultado el 3 de junio de 2010.
Bibliografía
editar- MacCluer, Barbara D. (2009). Elementary Functional Analysis. Springer. ISBN 978-1-4419-2753-8.
- Marsden; Tromba (2003). Vector Calculus (5ª edición). Springer. ISBN 978-0-7167-4992-9.
- Meyer, Carl D. (2000). Matrix Analysis and Applied Linear Algebra. SIAM. ISBN 978-0-898714-54-8.
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7
|isbn=incorrecto (ayuda). - Resnick, Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6.ª edición). Brooks/Cole. ISBN 0-534-40842-7.
- Shafarevich; Remizov (2013). Linear Algebra and Geometry (1ª ed trad. al inglés (ebook) edición). Springer. ISBN 978-3-642-30994-6.
- Strang, Gilbert (2009). Introduction to Linear Algebra (en inglés) (4.ª intl. edición). Wellesley-Cambridge Press. ISBN 978-0-9802327-2-1.
- Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
Enlaces externos
editar- Wikcionario tiene definiciones y otra información sobre vector.
- Weisstein, Eric W. «Vector». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.















